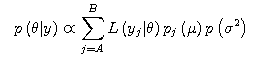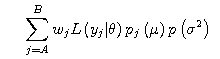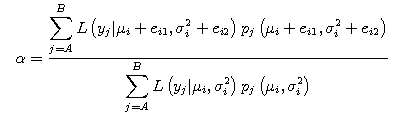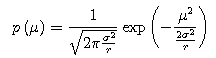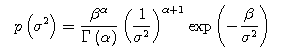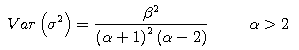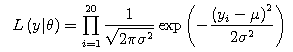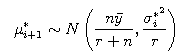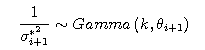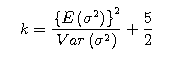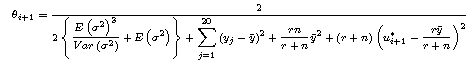This article is principally indebted to the works of Yoshiyuki Wakui, who is Japanese researcher in mathematics, in the same way as Part 1. I experimentally introduced the bimodal distribution to the research and
I'd very much appreciate the useful descriptions.
First I also tentatively outline the situation we were put in. Someone who was busy with his work generated two sorts of normal random numbers with a computer. One followed N(-0.7,1) and the other followed N(0.7,1).
As his phone abruptly rang, he had to deal with something urgent. After a while he realized he clean forgot the variances of the normal random variables and barely remembered the population means of the data sets
and the distributions of the data sets. Unfortunately, he needed to generate the additional normal random numbers which followed the almost same normal distributions.
1. The Data Sets
The data sets he generated at that time is given below.
| n | 1 | 2 | 3 | 4 | 5 |
| yA | -2.18 | -1.19 | -0.74 | -1.2 | -2.53 |
| n | 6 | 7 | 8 | 9 | 10 |
| yA | -0.5 | 0.09 | 0.31 | -1.71 | -0.67 |
| n | 11 | 12 | 13 | 14 | 15 |
| yB | 0.59 | 0.13 | 1.22 | 0.45 | -0.22 |
| n | 16 | 17 | 18 | 19 | 20 |
| yB | 0.15 | 1.5 | 1.06 | 1.32 | 1.88 |
The unstratified sample mean is about -0.11 and the unstratified and unbiased sample variance is about 1.52. Number 1-10, yA are actually generated from the normal distribution N(-0.7,1) and number 11-20, yB are generated from the normal distribution N(0.7,1). He clean forgot the population variances of the data sets but fortunately remembered the population means of the data sets, yA and yB. That is to say we pretend to forget the population variances of the data sets, yA and yB.
2. The Estimation of The Prior Distribution
I supposed that the population mean μ of the random variables y followed the bimodal distribution, that the
population mean μA of the random variables yA and
the population mean μB of the random variables yB
followed the different normal distributions, that the hyperparameter, which was the probability that the population mean of the 10 random variables yA of the 20 random variables y took the population mean μA, was set to 0.5, that the hyperparameter, which was
the probability that the population mean of the 10 random variables yB of the 20 random variables y took the population mean μB, was set to 0.5, that the population mean μA was -0.7, that the population mean μB was 0.7, that the population
variance of μA and μB was in proportion to the
population variance σ2 of the random variables y, and that the population variance σ2 of the random variables y followed the inverse gamma distribution. The example of the prior distribution is given below.
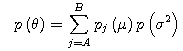
We substitute pA(μ), B(μ), and p(σ2) in the above equation to find the prior distribution.
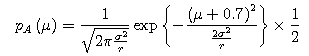
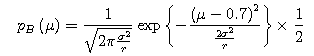
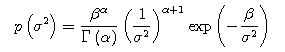
We also substitute the parameters for both E(σ2)
and Var(σ2) in the below equations to find the
value of both α and β.
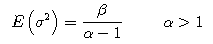
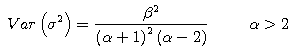
source code: PriorMultiModal.java
import java.awt.*;
import java.awt.event.*;
import java.applet.Applet;
import javax.swing.JLabel;
import javax.swing.JTextField;
public class PriorMultiModal extends Applet implements ActionListener{
// variable set
private static final long serialVersionUID = -3846703423854379608L;
final static int StartingX=50,StartingY=527;
final static String[] rulerX = {"",""," -1.6",""," -0.8", ""," 0",""," 0.8",""," 1.6",""};
final static String[] rulerY = {"",""," 0.2",""," 0.6", ""," 1.0",""," 1.4",""," 1.8",""};
final static String[] rulerZ = {"","","","",""," 0","","","","","","","",""};
final int EndingX=StartingX+transformation(120,120,120).x;
final int EndingY=StartingY+transformation(120,-120,-120).y;
public int[] SmallestInnerPart=new int[EndingX+1];
public int[] LargestInnerPart=new int[EndingX+1];
public static double exp = 1.0;
public static double var = 1.0;
public static double ratio = 3.0;
JTextField yx = new JTextField("1.0");
JTextField yn = new JTextField("1.0");
JTextField yr = new JTextField("3.0");
JLabel label1 = new JLabel("The Prior Distribution",JLabel.CENTER);
JLabel label2 = new JLabel("<html><body><font size=3>The Expectation of σ<sup>2</sup> (0<E(σ<sup>2</sup>)≤2.0)</font></body></html>", JLabel.CENTER);
JLabel label3 = new JLabel("<html><body><font size=3>The Variance of σ<sup>2</sup> (0<Var(σ<sup>2</sup>)≤10<sup>8</sup>)</font></body></html>", JLabel.CENTER);
JLabel label4 = new JLabel("<html><body><font size=3>The Ratio of σ<sup>2</sup> to Var(μ<sub>j</sub>) (0<r≤10<sup>8</sup>)</font></body></html>", JLabel.CENTER);
public void init(){
label1.setPreferredSize(new Dimension(400,24));
label1.setFont(new Font("Serif",Font.BOLD,15));
add(label1);
label2.setPreferredSize(new Dimension(260,23));
label2.setFont(new Font("Serif",Font.BOLD,11));
add(label2);
yx.setPreferredSize(new Dimension(120,23));
add(yx);
label3.setPreferredSize(new Dimension(260,23));
label3.setFont(new Font("Serif",Font.BOLD,11));
add(label3);
yn.setPreferredSize(new Dimension(120,23));
add(yn);
label4.setPreferredSize(new Dimension(260,23));
label4.setFont(new Font("Serif",Font.BOLD,11));
add(label4);
yr.setPreferredSize(new Dimension(120,23));
add(yr);
yx.addActionListener(this);
yn.addActionListener(this);
yr.addActionListener(this);
}
public void actionPerformed(ActionEvent e){
if(e.getSource()==yx){exp = Double.valueOf(yx.getText()).doubleValue();
if(exp <= 0 || exp > 2.0){exp=1.0;
}
}
if(e.getSource()==yn){var = Double.valueOf(yn.getText()).doubleValue();
if(var <= 0 || var > Math.pow(10.0,8))
{var=1.0;
}
}
if(e.getSource()==yr){ratio = Double.valueOf(yr.getText()).doubleValue();
if(ratio <= 0 || ratio > Math.pow(10.0,8))
{ratio=3.0;
}
}
yx.setText(""+exp);
yn.setText(""+var);
yr.setText(""+ratio);
repaint();
}
public void paint(Graphics g){
Point dot,dot1,dot2,dot3,dot4,dot5,dot6;
Graphics2D g2 = (Graphics2D)g;
GradientPaint gp1 = new GradientPaint(0, 0, new Color(154,181,228), 0,470,new Color(225,232,245), true);
g2.setPaint(gp1);
g2.fillRect(0,0,460,447);
super.paint(g);
// x axis
g.setColor(new Color(128,128,128));
dot1=transformation(-120,-120,0);
dot2=transformation(120,-120,0);
g.drawLine(dot1.x,dot1.y,dot2.x,dot2.y);
for(int i=0;i<21;i++){
dot1=transformation((120/10*i-120),-120,0);
if(i % 4==0){
dot2=transformation((120/10*i-120),(-120-10),0);
g.setColor(new Color(128,128,128));
g.drawLine(dot1.x,dot1.y,dot2.x,dot2.y);
g2.setFont(new Font ("SanSerif",Font.PLAIN,12));
g.drawString(rulerX[i/2],dot2.x-48,dot2.y+15);
if(i==8)
g.drawString("μ",dot2.x+28,dot2.y+30);
}
}
// y axis
g.setColor(new Color(128,128,128));
dot1=transformation(-120,-120,0);
dot2=transformation(-120,120,0);
dot3=transformation(-120,120,0);
dot4=transformation(-120,120,210);
dot5=transformation(120,-120,0);
dot6=transformation(120,120,0);
g.drawLine(dot1.x,dot1.y,dot2.x,dot2.y);
g.drawLine(dot3.x,dot3.y,dot4.x,dot4.y);
g.drawLine(dot5.x,dot5.y,dot6.x,dot6.y);
for(int i=0;i<210;i=i+1){
dot3=transformation(-119,120,i);
dot4=transformation(120,120,i);
g.setColor(new Color(154,181,228));
g.drawLine(dot3.x,dot3.y,dot4.x,dot4.y);
}
g.setColor(new Color(128,128,128));
for(int i=3;i<10;i++){
dot3=transformation(-120,120,(12/4*(i+3)-15)*10);
dot4=transformation(120,120,(12/4*(i+3)-15)*10);
g.drawLine(dot3.x,dot3.y,dot4.x,dot4.y);
}
for(int i=0;i<21;i++){
dot1=transformation(120,(12*i-120),0);
if(i % 4==0){
dot2=transformation((12+1)*10,(12*i-120),0);
g.setColor(new Color(128,128,128));
g.drawLine(dot1.x,dot1.y,dot2.x,dot2.y);
g.setFont(new Font ("SanSerif",Font.PLAIN,12));
g.drawString(rulerY[i/2],dot2.x-10,dot2.y+13);
if(i==8) g.drawString("σ",dot2.x+38,dot2.y+16);
g2.setFont(new Font ("SanSerif",Font.PLAIN,8));
if(i==8) g.drawString("2",dot2.x+47,dot2.y+9);
}
}
// z axis
g.setColor(new Color(128,128,128));
dot1=transformation(-120,-120,0);
dot2=transformation(-120,-120,210);
dot3=transformation(-120,119,210);
dot4=transformation(-120,119,0);
g.drawLine(dot1.x,dot1.y,dot2.x,dot2.y);
g.drawLine(dot2.x,dot2.y,dot3.x,dot3.y);
g.drawLine(dot3.x,dot3.y,dot4.x,dot4.y);
for(int i=0;i<240;i=i+1){
g.setColor(new Color(154,181,228));
dot5=transformation(-120,(-119+i),210);
dot6=transformation(-120,(-119+i),0);
g.drawLine(dot5.x,dot5.y,dot6.x,dot6.y);
}
g.setColor(new Color(128,128,128));
for(int i=2;i<10;i++){
dot1=transformation(-120,-120,(30*(i+3)-150));
dot2=transformation(-130,-120,(30*(i+3)-150));
dot3=transformation(-120,-119,(30*(i+3)-150));
dot4=transformation(-120,120,(30*(i+3)-150));
g.drawLine(dot1.x,dot1.y,dot2.x,dot2.y);
g.drawLine(dot3.x,dot3.y,dot4.x,dot4.y);
g2.setFont(new Font ("SanSerif",Font.PLAIN,12));
g.drawString(rulerZ[(i+3)],dot2.x-38,dot2.y+5);
if(i==5) g.drawString("L",dot2.x-25,dot2.y-110);
}
// Coloring
for(int i=0;i<=EndingX;i++){
SmallestInnerPart[i]=EndingY;
LargestInnerPart[i]=0;
}
dot=new Point();
for(double x=120;x>=-120;x-=0.2)
for(double y=-120;y<=120;y+=0.2){
double transX=x/60;
double transY=y/120+1;
double transZ=function(transX,transY);
double z=transZ*15.2;
dot=transformation(x,y,z);
if(dot.y<SmallestInnerPart[dot.x]){
SmallestInnerPart[dot.x]=dot.y;
g.setColor(gradation(z));
g.drawRect(dot.x,dot.y,1,1);
}
if(dot.y>LargestInnerPart[dot.x]){
LargestInnerPart[dot.x]=dot.y;
g.setColor(new Color(128,128,128));
g.drawRect(dot.x,dot.y,1,1);
}
}
}
public static double function(double x, double y){
double z;
double k0;
double k1;
double u;
u=Math.pow((2*Math.PI)*(y/ratio),(-0.5))*(Math.exp(-Math.pow((x-0.7),2)/(2*y/ratio))+Math.exp
(-Math.pow((x+0.7),2)/(2*y/ratio)))/2;
k0=Math.pow(exp,2)/var+2;
k1=Math.pow(exp,3)/var+exp;
z=Math.pow(y,(-k0-1))*Math.exp((-k1)/(y))*u;
if(y>=0){
if(z>=0){
if(u>=0)
return 80*z;
else return 0;
}
else return 0;
}
else return 0;
}
public Color gradation(double z){
int d,r,g,b;
z=z*5.2;
if(z>=0) d=(int)z % 256;
else d=255-(-(int)z % 256);
int c=(int)(d/85.334);
switch(c){
case 0: r=79+76*d/86;
g=129+58*d/86;
b=189-100*d/86;
break;
case 1: r=155+37*(d-86)/85;
g=187-99*(d-86)/85;
b=89-12*(d-86)/85;
break;
case 2: r=192-113*(d-171)/84;
g=88+41*(d-171)/84;
b=77+112*(d-171)/84;
break;
default: r=0; g=0; b=0;
break;
}
Color color=new Color(r,g,b);
return color;
}
public Point transformation(double x,double y,double z){
Point dot=new Point();
dot.x=StartingX+(int)((x+120)+Math.cos(Math.toRadians(30))*(y+120)/2);
dot.y=StartingY-(int)(Math.sin(Math.toRadians(30))*(y+120)/2+(z+120));
return dot;
}
}
3. The Estimation of The Posterior Distribution
The example of the conditional likelihood function is given below.
![$$L\left( y_A|\theta \right) = \prod_{i=1}^{10}{\left[ \frac{1}{\sqrt{2\pi\sigma^2}} \exp{\left( -\frac{\left( y_i-\mu\right)^2}{2\sigma^2} \right)}\times \frac{1}{2}\right] }$$ $$L\left( y_A|\theta \right) = \prod_{i=1}^{10}{\left[ \frac{1}{\sqrt{2\pi\sigma^2}} \exp{\left( -\frac{\left( y_i-\mu\right)^2}{2\sigma^2} \right)}\times \frac{1}{2}\right] }$$](http://paulownia.sakura.ne.jp/materials/learning_journals/archives/eqn18.png)
![$$L\left( y_B|\theta \right) = \prod_{i=11}^{20}{\left[ \frac{1}{\sqrt{2\pi\sigma^2}} \exp{\left( -\frac{\left( y_i-\mu\right)^2}{2\sigma^2} \right)}\times \frac{1}{2}\right] }$$ $$L\left( y_B|\theta \right) = \prod_{i=11}^{20}{\left[ \frac{1}{\sqrt{2\pi\sigma^2}} \exp{\left( -\frac{\left( y_i-\mu\right)^2}{2\sigma^2} \right)}\times \frac{1}{2}\right] }$$](http://paulownia.sakura.ne.jp/materials/learning_journals/archives/eqn19.png)
The posterior distribution is in proportion to the
product of the conditional likelihood function
multiplied by the prior distribution and the
example with weight wj is given below.
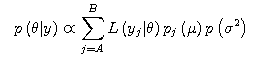
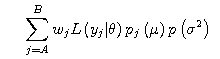
source code: PosteriorMultiModal.java
import java.awt.*;
import java.awt.event.*;
import java.applet.Applet;
import javax.swing.JLabel;
import javax.swing.JTextField;
public class PosteriorMultiModal extends Applet implements
ActionListener{
// variable set
private static final long serialVersionUID = -3578181170658236841L;
final static int StartingX=50,StartingY=527;
final static String[] rulerX = {"",""," -1.6",""," -0.8",""," 0",""," 0.8",""," 1.6",""};
final static String[] rulerY = {"",""," 0.2",""," 0.6",""," 1.0",""," 1.4",""," 1.8",""};
final static String[] rulerZ = {"","","","",""," 0","","","","","","","",""};
final int EndingX=StartingX+transformation(120,120,120).x;
final int EndingY=StartingY+transformation(120,-120,-120).y;
public int[] SmallestInnerPart=new int[EndingX+1];
public int[] LargestInnerPart=new int[EndingX+1];
public static double exp = 1.0;
public static double var = 1.0;
public static double ratio = 10.0;
JTextField yx = new JTextField("1.0");
JTextField yn = new JTextField("1.0");
JTextField yr = new JTextField("10.0");
JLabel label1 = new JLabel("The Posterior Distribution",JLabel.CENTER);
JLabel label2 = new JLabel("<html><body><font size=3>The Expectation of σ<sup>2</sup> (0<E(σ<sup>2</sup>)≤2.0)/font></body></html>", JLabel.CENTER);
JLabel label3 = new JLabel("<html><body><font size=3>The Variance of σ<sup>2</sup> (0<Var(σ<sup>2</sup>)≤10<sup>8</sup>)</font></body></html>", JLabel.CENTER);
JLabel label4 = new JLabel("<html><body><font size=3>The Ratio of σ<sup>2</sup> to Var(μ<sub>j</sub>) (0<r≤
10<sup>8</sup>)</font></body></html>", JLabel.CENTER);
public void init(){
label1.setPreferredSize(new Dimension(400,24));
label1.setFont(new Font("Serif",Font.BOLD,15));
add(label1);
label2.setPreferredSize(new Dimension(260,23));
label2.setFont(new Font("Serif",Font.BOLD,11));
add(label2);
yx.setPreferredSize(new Dimension(120,23));
add(yx);
label3.setPreferredSize(new Dimension(260,23));
label3.setFont(new Font("Serif",Font.BOLD,11));
add(label3);
yn.setPreferredSize(new Dimension(120,23));
add(yn);
label4.setPreferredSize(new Dimension(260,23));
label4.setFont(new Font("Serif",Font.BOLD,11));
add(label4);
yr.setPreferredSize(new Dimension(120,23));
add(yr);
yx.addActionListener(this);
yn.addActionListener(this);
yr.addActionListener(this);
}
public void actionPerformed(ActionEvent e){
if(e.getSource()==yx){exp = Double.valueOf(yx.getText()).doubleValue();
if(exp <= 0 || exp > 2.0){exp=1.0;
}
}
if(e.getSource()==yn){var = Double.valueOf(yn.getText()).doubleValue();
if(var <= 0 || var > Math.pow(10.0,8)){var=1.0;
}
}
if(e.getSource()==yr){ratio = Double.valueOf(yr.getText()).doubleValue();
if(ratio <= 0 || ratio > Math.pow(10.0,8))
{ratio=10.0;
}
}
yx.setText(""+exp);
yn.setText(""+var);
yr.setText(""+ratio);
repaint();
}
public void paint(Graphics g){
Point dot,dot1,dot2,dot3,dot4,dot5,dot6;
Graphics2D g2 = (Graphics2D)g;
GradientPaint gp1 = new GradientPaint(0, 0, new Color(154,181,228), 0,470,new Color(225,232,245), true);
g2.setPaint(gp1);
g2.fillRect(0,0,460,447);
super.paint(g);
// x axis
g.setColor(new Color(128,128,128));
dot1=transformation(-120,-120,0);
dot2=transformation(120,-120,0);
g.drawLine(dot1.x,dot1.y,dot2.x,dot2.y);
for(int i=0;i<21;i++){
dot1=transformation((120/10*i-120),-120,0);
if(i % 4==0){
dot2=transformation((120/10*i-120),(-120-10),0);
g.setColor(new Color(128,128,128));
g.drawLine(dot1.x,dot1.y,dot2.x,dot2.y);
g2.setFont(new Font ("SanSerif",Font.PLAIN,12));
g.drawString(rulerX[i/2],dot2.x-48,dot2.y+15);
if(i==8)
g.drawString("μ",dot2.x+28,dot2.y+30);
}
}
// y axis
g.setColor(new Color(128,128,128));
dot1=transformation(-120,-120,0);
dot2=transformation(-120,120,0);
dot3=transformation(-120,120,0);
dot4=transformation(-120,120,210);
dot5=transformation(120,-120,0);
dot6=transformation(120,120,0);
g.drawLine(dot1.x,dot1.y,dot2.x,dot2.y);
g.drawLine(dot3.x,dot3.y,dot4.x,dot4.y);
g.drawLine(dot5.x,dot5.y,dot6.x,dot6.y);
for(int i=0;i<210;i=i+1){
dot3=transformation(-119,120,i);
dot4=transformation(120,120,i);
g.setColor(new Color(154,181,228));
g.drawLine(dot3.x,dot3.y,dot4.x,dot4.y);
}
g.setColor(new Color(128,128,128));
for(int i=3;i<10;i++){
dot3=transformation(-120,120,(12/4*(i+3)-15)*10);
dot4=transformation(120,120,(12/4*(i+3)-15)*10);
g.drawLine(dot3.x,dot3.y,dot4.x,dot4.y);
}
for(int i=0;i<21;i++){
dot1=transformation(120,(12*i-120),0);
if(i % 4==0){
dot2=transformation((12+1)*10,(12*i-120),0);
g.setColor(new Color(128,128,128));
g.drawLine(dot1.x,dot1.y,dot2.x,dot2.y);
g.setFont(new Font ("SanSerif",Font.PLAIN,12));
g.drawString(rulerY[i/2],dot2.x-10,dot2.y+13);
if(i==8) g.drawString("σ",dot2.x+38,dot2.y+16);
g2.setFont(new Font ("SanSerif",Font.PLAIN,8));
if(i==8) g.drawString("2",dot2.x+47,dot2.y+9);
}
}
// z axis
g.setColor(new Color(128,128,128));
dot1=transformation(-120,-120,0);
dot2=transformation(-120,-120,210);
dot3=transformation(-120,119,210);
dot4=transformation(-120,119,0);
g.drawLine(dot1.x,dot1.y,dot2.x,dot2.y);
g.drawLine(dot2.x,dot2.y,dot3.x,dot3.y);
g.drawLine(dot3.x,dot3.y,dot4.x,dot4.y);
for(int i=0;i<240;i=i+1){
g.setColor(new Color(154,181,228));
dot5=transformation(-120,(-119+i),210);
dot6=transformation(-120,(-119+i),0);
g.drawLine(dot5.x,dot5.y,dot6.x,dot6.y);
}
g.setColor(new Color(128,128,128));
for(int i=2;i<10;i++){
dot1=transformation(-120,-120,(30*(i+3)-150));
dot2=transformation(-130,-120,(30*(i+3)-150));
dot3=transformation(-120,-119,(30*(i+3)-150));
dot4=transformation(-120,120,(30*(i+3)-150));
g.drawLine(dot1.x,dot1.y,dot2.x,dot2.y);
g.drawLine(dot3.x,dot3.y,dot4.x,dot4.y);
g2.setFont(new Font ("SanSerif",Font.PLAIN,12));
g.drawString(rulerZ[(i+3)],dot2.x-38,dot2.y+5);
if(i==5) g.drawString("L",dot2.x-25,dot2.y-110);
}
// Coloring
for(int i=0;i<=EndingX;i++){
SmallestInnerPart[i]=EndingY;
LargestInnerPart[i]=0;
}
dot=new Point();
for(double x=120;x>=-120;x-=0.2)
for(double y=-120;y<=120;y+=0.2){
double transX=x/60;
double transY=y/120+1;
double transZ=function(transX,transY);
double z=transZ*3.8;
dot=transformation(x,y,z);
if(dot.y<SmallestInnerPart[dot.x]){
SmallestInnerPart[dot.x]=dot.y;
g.setColor(gradation(z));
g.drawRect(dot.x,dot.y,1,1);
}
if(dot.y>LargestInnerPart[dot.x]){
LargestInnerPart[dot.x]=dot.y;
g.setColor(new Color(128,128,128));
g.drawRect(dot.x,dot.y,1,1);
}
}
}
public static double function(double x, double y){
double z1;
double z2;
double k0;
double k1;
double u1;
double u2;
double d01=1;
double d02=1;
double[] d1= new double[21];
double[] d2={-2.18,-1.19,-0.74,-1.2,-2.53,-0.5,0.09,0.31,-1.71,-0.67};
double[] d3= new double[21];
double[] d4= {0.59,0.13,1.22,0.45,-0.22,0.15,1.5,1.06,1.32,1.88};
for(int i=0;i<10;i++){
d1[i]=Math.pow(2*Math.PI*y,(-0.5))*Math.exp(-Math.pow((d2[i]-x),2)/(2*y));
d01=2.4*d01*d1[i];
}
for(int i=0;i<10;i++){
d3[i]=Math.pow(2*Math.PI*y,(-0.5))*Math.exp(-Math.pow((d4[i]-x),2)/(2*y));
d02=2.4*d02*d3[i];
}
u1=Math.pow((2*Math.PI)*(y/ratio),(-0.5))*Math.exp(-Math.pow((x+0.7),2)/(2*y/ratio));
u2=Math.pow((2*Math.PI)*(y/ratio),(-0.5))*Math.exp(-Math.pow((x-0.7),2)/(2*y/ratio));
k0=Math.pow(exp,2)/var+2;
k1=Math.pow(exp,3)/var+exp;
z1=9*Math.pow(y,(-k0-1))*Math.exp((-k1)/(y))*u1;
z2=9*Math.pow(y,(-k0-1))*Math.exp((-k1)/(y))*u2;
if(y>=0){
if(z1>=0 && z2>=0){
if(u1>=0 && u2>=0)
return 1200*d01*z1+36*d02*z2;
else return 0;
}
else return 0;
}
else return 0;
}
public Color gradation(double z){
int d,r,g,b;
z=z*5.2;
if(z>=0) d=(int)z % 256;
else d=255-(-(int)z % 256);
int c=(int)(d/85.334);
switch(c){
case 0: r=79+76*d/86;
g=129+58*d/86;
b=189-100*d/86;
break;
case 1: r=155+37*(d-86)/85;
g=187-99*(d-86)/85;
b=89-12*(d-86)/85;
break;
case 2: r=192-113*(d-171)/84;
g=88+41*(d-171)/84;
b=77+112*(d-171)/84;
break;
default: r=0; g=0; b=0;
break;
}
Color color=new Color(r,g,b);
return color;
}
public Point transformation(double x,double y,double z){
Point dot=new Point();
dot.x=StartingX+(int)((x+120)+Math.cos(Math.toRadians(30))*(y+120)/2);
dot.y=StartingY-(int)(Math.sin(Math.toRadians(30))*(y+120)/2+(z+120));
return dot;
}
}
4. The Metropolis Sampler algorithm
The example of the Metropolis sampler is given
below.
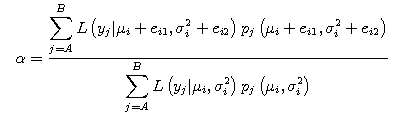
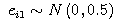
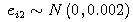
We accept μ*i+1 and σ*2i+1 when α meets the below conditions.

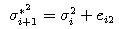
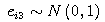
We reject the above μ* i+1 and σ*2i+1 and accept the below μ*i+1 and σ*2i+1 when α meets the below condition.

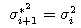
source code: Metropolis.java
import java.awt.*;
import java.awt.event.*;
import java.text.DecimalFormat;
import java.applet.Applet;
import javax.swing.JLabel;
import javax.swing.JTextField;
public class Metropolis extends Applet implements ActionListener{
// variable set
private static final long serialVersionUID = 8565245775496766530L;
public static double exp = 1.0;
public static double var = 1.0;
public static double ratio = 10.0;
public static double u, d3, d4, d7, d8, d9, d10, d11, d12;
public static double[] s1 = new double[10000];
public static double[] s2 = new double[10000];
public static double[] s3 = new double[1000];
public static double[] s4 = new double[1000];
public static double[] se1 = new double[10000];
public static double[] se2 = new double[10000];
public static double[] d1 = new double[10000];
public static double[] d2 = new double[10000];
public static double[] d5 = new double[10000];
public static double[] d6 = new double[10000];
JTextField yx = new JTextField("1.0");
JTextField yn = new JTextField("1.0");
JTextField yr = new JTextField("10.0");
JLabel label1 = new JLabel("The Metropolis Sampler Frequency Distribution",JLabel.CENTER);
JLabel label2 = new JLabel("<html><body><font size=3>The Expectation of σ<sup>2</sup> (0<E(σ<sup>2</sup>)≤10<sup>8</sup>)</font></body></html>",JLabel.CENTER);
JLabel label3 = new JLabel("<html><body><font size=3>The Variance of σ<sup>2</sup> (0<Var(σ<sup>2</sup>)≤10<sup>8</sup>)</font></body></html>",JLabel.CENTER);
JLabel label4 = new JLabel("<html><body><font size=3>The Ratio of σ<sup>2</sup> to Var(μ<sub>j</sub>) (0<r≤10<sup>8</sup>)</font></body></html>", JLabel.CENTER);
public void init(){
label1.setPreferredSize(new Dimension(416,24));
label1.setFont(new Font("Serif",Font.BOLD,14));
add(label1);
label2.setPreferredSize(new Dimension(260,23));
label2.setFont(new Font("Serif",Font.BOLD,11));
add(label2);
yx.setPreferredSize(new Dimension(80,23));
add(yx);
label3.setPreferredSize(new Dimension(260,23));
label3.setFont(new Font("Serif",Font.BOLD,11));
add(label3);
yn.setPreferredSize(new Dimension(80,23));
add(yn);
label4.setPreferredSize(new Dimension(260,23));
label4.setFont(new Font("Serif",Font.BOLD,11));
add(label4);
yr.setPreferredSize(new Dimension(80,23));
add(yr);
yx.addActionListener(this);
yn.addActionListener(this);
yr.addActionListener(this);
}
public void actionPerformed(ActionEvent e){
if(e.getSource()==yx){
exp=Double.valueOf(yx.getText()).doubleValue();
if(exp <= 0 || exp > Math.pow(10.0,8)){
exp = 1.0;
}
}
if(e.getSource()==yn){
var = Double.valueOf(yn.getText()).doubleValue();
if(var <= 0 || var > Math.pow(10.0,8)){
var = 1.0;
}
}
if(e.getSource()==yr){ratio = Double.valueOf(yr.getText()).doubleValue();
if(ratio <= 0 || ratio > Math.pow(10.0,8))
{ratio = 10.0;}
}
yx.setText(""+exp);
yn.setText(""+var);
yr.setText(""+ratio);
repaint();
}
public void paint(Graphics g){
double z1,z2,ss1,ss2;
s1[0] = 0.0;
s2[0] = 1.0;
z1=function(s1[0],s2[0]);
for(int i=0;i<9999;i++){
se1[i]=normal.sampleNormal(0,0.5);
se2[i]=normal.sampleNormal(0,0.002);
ss1=s1[i]+se1[i];
ss2=s2[i]+se2[i];
z2=function(ss1,ss2);
if(z2/z1>=1){
s1[i+1]=ss1;
s2[i+1]=ss2;
z1=z2;
}
else if(z2/z1>=normal.sampleNormal(0,1)){
s1[i+1]=ss1;
s2[i+1]=ss2;
z1=z2;
}
else {
s1[i+1]=s1[i];
s2[i+1]=s2[i];
}
}
d1[5000]=s1[5000];
d2[5000]=s2[5000];
for(int i=5001;i<10000;i++){
d1[i]=d1[i-1]+s1[i];
d2[i]=d2[i-1]+s2[i];
}
d3=d1[9999]/5000;
d4=d2[9999]/5000;
d5[4999]=0;
d6[4999]=0;
for(int i=5000;i<10000;i++){
d5[i]=Math.pow((s1[i]-d3),2)+d5[i-1];
d6[i]=Math.pow((s2[i]-d4),2)+d6[i-1];
}
d7=d5[9999]/(5000-1);
d8=d6[9999]/(5000-1);
// variable set
int[] xxxx = new int[1000];
int[] yyyy = new int[1000];
int[] xxxx1 = new int[1000];
int[] yyyy1 = new int[1000];
double minss1 = s1[5000];
double maxss1 = s1[5000];
double minss2 = s2[5000];
double maxss2 = s2[5000];
for(int i=5000;i<10000;i++){
if(s1[i]>maxss1){
maxss1 = s1[i];
}
}
for(int i=5000;i<10000;i++){
if(s1[i]<minss1){
minss1 = s1[i];
}
}
for(int i=5000;i<10000;i++){
if(s2[i]>maxss2){
maxss2 = s2[i];
}
}
for(int i=5000;i<10000;i++){
if(s2[i]<minss2){
minss2 = s2[i];
}
}
for(int i=0;i<1000;i++){
s3[i]=0;
s4[i]=0;
}
double aaa=(maxss1-minss1)/1000;
double bbb=(maxss2-minss2)/1000;
for(int i=5000;i<10000;i++){
for(int j=0;j<1000;j++){
if(s1[i] >= (minss1+aaa*j) && s1[i] < minss1+aaa*(j+1))
s3[j]=(s3[j]+1.0);
}
}
for(int i=5000;i<10000;i++){
for(int j=0;j<1000;j++){
if(minss2+bbb*j<=s2[i] && s2[i] < minss2+bbb*(j+1))
s4[j]=s4[j]+1;
}
}
// variable set
double minss3 = s3[0];
double maxss3 = s3[0];
double minss4 = s4[0];
double maxss4 = s4[0];
for(int i=0;i<1000;i++){
if(maxss3<s3[i]){
maxss3 = s3[i];
}
}
for(int i=0;i<1000;i++){
if(s3[i]<minss3){
minss3 = s3[i];
}
}
for(int i=0;i<1000;i++){
if(s4[i]>maxss4){
maxss4 = s4[i];
}
}
for(int i=0;i<1000;i++){
if(s4[i]<minss4){
minss4 = s4[i];
}
}
double yyy = maxss3-minss3;
double yyy1 = maxss4-minss4;
for(int i=0;i<1000;i++){
xxxx[i] = (int)(i*351/1000)+33;
yyyy[i] = 474-(int)((s3[i]-minss3)*351/yyy);
xxxx1[i] = (int)(i*351/1000)+33;
yyyy1[i] = 474-(int)((s4[i]-minss4)*351/yyy1);
}
Graphics2D g2 = (Graphics2D)g;
GradientPaint gp1 = new GradientPaint(0, 0, new Color(154,181,228), 0,470,new Color(225,232,245), true);
g2.setPaint(gp1);
g2.fillRect(0,0,416,503);
super.paint(g);
GradientPaint gp2 = new GradientPaint(0, 33, new Color(225,232,245), 0,351,new Color(154,181,228),true);
g2.setPaint(gp2);
g2.fillRect(33,123,354,351);
GradientPaint gp4 = new GradientPaint(33, 227, new Color(192,88,77), 33,418,new Color(160,82,45), true);
g2.setPaint(gp4);
for (int i=0;i<1000;i++){
g2.drawLine(xxxx[i], 474, xxxx[i], yyyy[i]);
}
DecimalFormat df = new DecimalFormat("0.00");
g2.setFont(new Font ("Serif",Font.BOLD,12));
g2.setColor (new Color(0,0,0));
g2.drawString("n = 5000",280,157);
g2.setColor (new Color(0,0,0));
g2.setFont(new Font ("Serif",Font.BOLD,12));
g2.drawString("E(μ",280,177);
g2.setFont(new Font ("Serif",Font.BOLD,12));
g2.drawString("*",300,176);
g2.setFont(new Font ("Serif",Font.BOLD,12));
g2.drawString("|y) =",305,177);
g2.drawString(df.format(d3),335,177);
g2.drawString("Var(μ",280,197);
g2.setFont(new Font ("Serif",Font.BOLD,12));
g2.drawString("*",312,196);
g2.setFont(new Font ("Serif",Font.BOLD,12));
g2.drawString("|y) =",317,197);
g2.drawString(df.format(d7),347,197);
g2.setColor (new Color(0,0,0));
g2.drawString("E(σ",280,217);
g2.setFont(new Font ("Serif",Font.BOLD,12));
g2.drawString("*",300,216);
g2.setFont(new Font ("Serif",Font.BOLD,8));
g2.drawString("2",305,212);
g2.setFont(new Font ("Serif",Font.BOLD,12));
g2.drawString("|y) =",310,217);
g2.drawString(df.format(d4),340,217);
g2.drawString("Var(σ",280,237);
g2.setFont(new Font ("Serif",Font.BOLD,12));
g2.drawString("*",312,236);
g2.setFont(new Font ("Serif",Font.BOLD,8));
g2.drawString("2",317,232);
g2.setFont(new Font ("Serif",Font.BOLD,12));
g2.drawString("|y) =",322,237);
g2.drawString(df.format(d8),352,237);
g2.drawString("E(y) = -0.11",280,257);
g2.drawString("Var(y) = 1.52",280,277);
g2.setColor (new Color(0,0,0));
g2.drawString("F",15,143);
g2.setColor (new Color(79,129,189));
g2.setColor (new Color(192,88,77));
g2.drawString("μ",360,488);
}
public static double function(double x, double y){
double z1;
double z2;
double k0;
double k1;
double u1;
double u2;
double d01=1;
double d02=1;
double[] f1= new double[10];
double[] f2={-2.18,-1.19,-0.74,-1.2,-2.53,-0.5,0.09,0.31,-1.71,-0.67};
double[] f3= new double[10];
double[] f4={0.59,0.13,1.22,0.45,-0.22,0.15,1.5,1.06,1.32,1.88};
for(int i=0;i<10;i++){
f1[i]=Math.pow(2*Math.PI*y,(-0.5))*Math.exp(-Math.pow(f2[i]-x,2)/(2*y));
d01=d01*f1[i];
}
for(int i=0;i<10;i++){
f3[i]=Math.pow(2*Math.PI*y,(-0.5))*Math.exp(-Math.pow(f4[i]-x,2)/(2*y));
d02=d02*f3[i];
}
u1=Math.pow((2*Math.PI)*(y/ratio),(-0.5))*(Math.exp(-Math.pow((x+0.7),2)/(2*y/ratio)));
u2=Math.pow((2*Math.PI)*(y/ratio),(-0.5))*(Math.exp(-Math.pow((x-0.7),2)/(2*y/ratio)));
k0=Math.pow(exp,2)/var+2;
k1=Math.pow(exp,3)/var+exp;
z1=Math.pow(k1,k0)/GammaF.gamma(k0)*Math.pow(y,(-k0-1))*Math.exp((-k1)/(y))*u1;
z2=Math.pow(k1,k0)/GammaF.gamma(k0)*Math.pow(y,(-k0-1))*Math.exp((-k1)/(y))*u2;
if(y>=0){
if(z1>=0 && z2>=0){
if(u1>=0 && u2>=0)
return (d01*z1+d02*z2)/2;
else return 0;
}
else return 0;
}
else return 0;
}
}
source code: normal.java
import java.util.*;
public class normal {
private static Random rnd = new Random(Calendar.getInstance().
getTimeInMillis()+Thread.currentThread().getId());
private static double u;
public static double sampleNormal(double e0, double e1) {
double e2;
e2=Math.pow(e1,(0.5));
u=e2*rnd.nextGaussian()+e0;
return u;
}
}
GammaF.java
// See the below website, copy and paste the class "Gamma".
// Then modify the code as necessary.
//
// http://www.cs.princeton.edu/introcs/91float/Gamma.java.html
//
// I express my appreciation for Robert Sedgewick
// and Kevin Wayne.
In conclusion, the posterior distribution is bimodal because the conditional likelihood function is set to the bimodal form and the prior distribution is bimodal. The variances of μ and σ2 on the posterior distribution is smaller than the variances of μ and σ2 on the prior distribution because the posterior distribution is in proportion to the product of the conditional likelihood function and depends on the scatteration of the data.
Finally I am happy to assist you in coding and simulating a random process with the MCMC algorithm in JAVA.
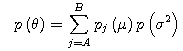
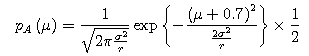
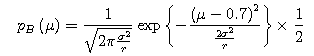
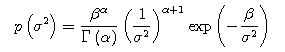
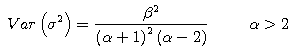
![$$L\left( y_B|\theta \right) = \prod_{i=11}^{20}{\left[ \frac{1}{\sqrt{2\pi\sigma^2}} \exp{\left( -\frac{\left( y_i-\mu\right)^2}{2\sigma^2} \right)}\times \frac{1}{2}\right] }$$ $$L\left( y_B|\theta \right) = \prod_{i=11}^{20}{\left[ \frac{1}{\sqrt{2\pi\sigma^2}} \exp{\left( -\frac{\left( y_i-\mu\right)^2}{2\sigma^2} \right)}\times \frac{1}{2}\right] }$$](http://paulownia.sakura.ne.jp/materials/learning_journals/archives/eqn19.png)