アルミケースのシルバーに合うカラーのベゼルの内蔵ドライブを探していたのだが、2010年前後ぐらいからシルバー系の新品の入手が困難になっていたようで、ホワイトのPioneerのブルーレイ・ドライブをヤフオクでゲットすることになる。
動作確認済みとの触れ込みだったが、トレイの開閉がスムーズでない点と『ベルリン・コンサート』のブルーレイの『オテロ』から『カルメン』を再生する際に回転音に含まれる異音が大きくなる点が気になっていた。
トレイの開閉については、秋葉原の千石電商に向かい直径25mmの角ゴムベルトを購入し、ゴムベルトの太さについては1.6mmだとゴムの張力が強すぎてモーターが回らず、0.95mmだと軽快にトレイが開閉し、1.2mmだとやや重厚感を感じさせるトレイの開閉スピードになる点を確認しながら、ゴムベルトを交換することで修理完了。
特定のブルーレイ再生時における異音については、レンズ部の反射光を見ないように注意しながらブルーレイ・ドライブを分解掃除し、エアー・ダスターで内部に溜まったホコリ等を飛ばした後、軸に当たるスピンドル・モーター部分のディスクとの接触面と上蓋をウェット・ティッシュで拭いていき、一休み。
ファームウェアを1.13にアップした際のデフォルトの設定がパイオニアの静音モードだったからかもしれないが、ここまでの作業でWindows10でのブルーレイ再生時における異音は解消されており、残された課題はLinuxでブルーレイを再生する際に同様の現象が再現することであったが、カーネルを4.14.18から4.15.3にアップデートする過程でWindows10で実現されていたであろう静音モードが引き継がれるようになったからであろうか、Linuxでも異音は解消されることになった。
中古のBluray・DVDドライブの購入はコワイなと感じていたのだが、当面はこんな感じで手を加えていき、それでもドライブを認識しない等の故障に行き当たれば、それはそのときに新品を購入すればよいだろうとの見通しを抱いており、しばらくは様子をみていきたい。
それでは。
# 補足
ディスク再生時に異音が再発したので、シルバーストーンのケース下部にあるレールにドライブを収納する5インチベイをガチッとはめ込み、ネジをしっかり締めることによって、ドライブのがたつきを抑え、異音を解消することになった。ここに至るまでピックアップレンズのレーザー出力調整からレンズ下部のレールのメンテナンスまで気になった要素を1つずつチェックしていったのだが、物理現象として理解して対処していくことが問題解決の道につながったのだろうか。10年物のブルーレイ・ドライブなので今後も何か色々あるかもしれないが、それはその時に改めて。では。
コンピュータの最近の記事
statcounter.comによれば、Apr 2016-Apr 2017にかけてのOS Xの市場シェアは11.63%になり、Windows, Linuxのシェアはそれぞれ84.22%及び1.67%になる。
私が使っているFedoraのシェアの低さはOSのデバッグ関連情報を掘り下げる手間に起因していることが大きいのだが、Linuxマシンのパーツ選択の幅について言えば、Windowsマシンと遜色ない状況が形成されつつあるとの期待を抱きながらも、そこにラグがあることも否めない現状になる。
話を本題にもどすと、廉価版であるヘキサコアのMac Proの価格は税込み322,704円になり、搭載されているXeon E5のクロックは3.5GHz、メモリはDDR3の1,866MHzになり、最大消費電力が450Wになる。
このレベルでやりたいことを実現するマシンをDIYしようとすると、私ならヘキサコアでクロック3.2GHzのRyzen 5を選び、メモリはDDR4の2,666MHz overを選択し、最大消費電力について450Wを下回る水準に抑えることを念頭におく。またパフォーマンスを決定する要因の1つであるマシンの価格については100,000円前後に収めるだろう。
そしてマシンの選択に際して、多様な文化の容認・共存といった考え方をバックグラウンドにMac Proを勧めるならば、その立場はLinuxマシンで代替でき、コスト・性能を理由にしてMac Proを勧めるならば、その立場はDIYマシンで代替できることになる。
しかし、それでもMac Proを購入する人達は一定数存在しており、大学関係者にその分布が偏っていることが示唆することの含意は、合理主義より権威主義が支配的な業界の特徴がそこに顕在化した結果であるかもしれないといった視点とともに、Mac Proではないものの「学部のマシンを一新するに際して情報学科の教員が一致団結してMacを導入しました」といったケースでは、初心者に対するサポートを名目に掲げたために却って学生にしわ寄せが来てしまった結果になるかもしれないといったことを考えることがあった。
それでは。
2008年3月頃から1日4時間程使用していたInspiron531sの電源ユニットはBestec製のTFX0250P5Wになるが、コンセントにプラグを差し、電源ユニットの裏にある緑のインジケーターが点灯するまでに1〜5分かかっていたことが最近確認されたため、電源ユニットの不具合を懸念していた。また、数年前のスリムケースのせいか出力が250Wであったことからか、300W以上の電源ユニットに交換することが電源ユニットの使用に対するゆとりを感じさせる運びとなっていた。
他方でエナジーセービングと言っても電気をこまめに消すことが全てではなく、例えば2004年に発表された80PLUSプログラムのように交流から直流に変換する際のエネルギー効率を高めることによって、消費電力を抑えていくといった思想に技術の進歩を感じるときがあった。メーカーの謳い文句によれば、1日4時間212Whの使用で、70%効率の電源ユニットと比較すると計算の前提にもよるが年間の電気料金が1,204円ほど安くなるといったことを考慮すると、Inspiron531sの電源ユニットが完全に故障していた訳ではなかったものの、近年の日本政府、産業界やメディアの広報キャンペーンが語ることが少ないエナジーセービングの在り方といったものを身近なところでささやかに実現することに魅力を感じることにつながっていた。下の写真はTFXに合わせたPS2-T350EFのパッケージになる。

ケーブルやコネクタは、ATX MAIN(20+4ピン)×1、ATX12V CPU(4ピン)×1、HDD ODD(4ピン)×3、FDD(4ピン)×1、SATA Ⅰ,Ⅱ×3になり、サイズはL175×W85×H65mmになるが、SATA用の電源ケーブルの長さに関し2本は約30cm前後あったが、残り1本は約15cm前後になり、DVDドライブに加えHDDを2台積んでいると、延長ケーブルを追加購入する必要があったことを追記したい。下の写真は本体とその付属品を示している。

熱やエアフローといったものを考慮するにはスリムケースではやや厳しいものになるが、下の写真は電源ユニット交換前のInspiron531sの内部構造になり、左上が光学ドライブ、右上がHDD、左下がCPUで、右下にあるシルバーのパーツが電源ユニットになる。

下の写真は交換後の内部構造になり、配線の配置が乱雑気味だが、右下にあるブラックのパーツがPS2-T350EFになり、ケースに固定するための3つのねじ穴も丁度良く合わせることができたことを追記したい。

最後に、電源ユニットを交換しトラブルを解消したのみならず、出力を100W増加させたにもかかわらず、実際の消費電力の軽減に繋がった事例に至ったことは、ともすれば4年という短い年月の経過の間に世界で生じていた技術進歩の恩恵だろうと考えることがあり、ここに感謝の言葉を申し添えたい。
では。
現在予断を許さない状況だが、アクセスポイントを
増やすことは好ましいことではないかと考えることが
あり、一筆する次第。
AFN(米軍放送)で流されていたことだが、横田
基地では犠牲者が0だったといったことに関し、地域
によって差が大きい問題であるが、横の絆を増やす
ことが求められていると考えるときがある。
# 補足
3/12(土)現在、千葉県北西部郊外では、小規模の書店
(オークスブックセンター白井駅前店)が休業中、また
ホームセンター(ホーマック、白井店)が休業中だった
が、ケーズデンキ白井駅前店は営業中だったことを追記
する(営業時間の変更については未確認)。
そしてIIBCからのアナウンスにより、第161回TOEICは
中止になったが、他方高校生・浪人生向けの試験として、
東大が後期試験を実施することを選択したことに対して、
他に妥当な選択肢が存在しないだろうかと考えることが
あり、外野から一々口を挟まれたくないとの立場を理解
してはいるものの、それでも少々周囲から振り返るべき
ことはないだろうかと考えることがある。
# 補足-2
3/13(日)現在、オークスブックセンター白井駅前店、
ホーマック白井店、共に営業していたが、天井にある
空調機が落下した痕跡、全ブロックが照明で照らされ
ている訳ではなく電気の明かりのない売り場ブロック
から示される通り、現在復旧中との印象を受けた。又、
2000円以下の携帯ラジオが売り切れで、やはりなとの
思いを抱くことがあった。
# 補足-3
3/14(月)現在、地元のホームセンターの開店時間前に
100人規模の行列ができていた。そして開店と共に、
乾電池売り場に人が殺到していたが、「乾電池は全て
売り切れです」との店員からのアナウンスがあった。
阪神・淡路大震災の教訓を思い起こせば、売り切れの
商品に関し1週間もすれば在庫分が入荷されるだろうと
考えることがあり、関西及び中京地区の生産流通能力
を信頼し待つしかないだろう。仕事は計画停電のために
休みとなったが、今後次第であることに変わりはない。
それでは。
# update-rc.d networking defaults は有線LANのケースに
なり、そして # update-rc.d wicd defaults は無線LANのケース
になるものの、今更ながらの話だがそれだけではうまくいかな
いケースの参考になれば良しとしたいとの思いがある。
# /etc/init.d/wicd start
# /usr/bin/start-network
# /usr/bin/wicd-client on
上記のコマンドにより問題が解決されたが、海外サイトの手
引きに色々書かれてあることとその情報量の多さを鑑み、ここ
ではこれぐらいの紹介に止めるが、ネットワークマネージャー
を起動させることができれば後は自力で何とかなるだろう。
ここからが今日の課題。
TOEIC対策は模試。正答率は、パート3が21/20、パート4が
6/12、パート6が10/12で、パート7が22/28。Rの時間は累計45
分で、ダブルパッセージに30分かけることができる。
伊検対策は作文と聞き取り。作文は伊文筆写を40本ほど。
こんなペースだが伊文と格闘するといった段階ではなく、
徐々に親しみをおぼえるよう慣らしている状況か。
明日もがんばろう。
では。
先日、GeForce8400GSが故障し、グラフィックボードを
GeForce210に交換したのだが、国内のサイトでの動作報告
を見る限り、GeForce210とOracle Solaris 11 Expressとの
相性が悪く、バグを内包しているため、通常の方法ではXが
起動しないとの記事が散見された。
しかし、以下のBugzillaを見る限り、ドライバの更新に
より不具合を克服する対処法があることに気が付いた。
https://defect.opensolaris.org/bz/show_bug.cgi?id=15751
具体的には、nvidia.comのサイトから、DOWNLOAD
DRIVERS→Beta and Archived Driversを選択し、GeForce
210の代わりにGeForceG210を選択すると、NVIDIA-Solaris-
x86-270.26.runがダウンロードできる状態になる。
後は、# sh ./NVIDIA-Solaris-x86-270.26.run 及び、
# nvidia-xconfigで、無事にXを立ち上げることができる
様になったことを追記する。
Fedora14の場合も同様だが、270.26のバージョンに
より、Emerald及びScreenletsの不具合が解消されたの
は朗報に聞こえるかもしれない。
実際の所、シングルユーザーモードでの起動から調査
を進めていたため(-sをカーネルパラメーターに加える
だけだが..)、まだやるべきことは沢山あるかなとの
感想を抱いたのだが、この程度ならば無事に事が運んで
良かったと言っても構わないだろう。
ここからが今日の課題。
英検対策は語彙とエッセイ。WSGREの正答率は、
4/17。impassive, imperturbable, 冷静な、implacable,
宥めにくい、arrest, 妨害、forestall, 妨害する、slake,
〜を満たす、whet, 〜を刺激する、fetter, 拘束、table,
審議延期にする、exact, 要求する、travesty, パロディー、
pervade, permeate, 広がる、pine, 切望、plangent,
押し寄せる、equanimity, self-possession, 落ち着き、
toady, sycophant, おべっか使い、epitome, 縮図、
cozen, 〜を騙す、等で失点しており、周回が必要か。
伊検対策はお休み。明日から再開する計画を
立てるが、こんなちょっとした息抜きがあっても
構わないだろうと考えることがある。
明日もがんばろう。
では。
I have recently and unfortunately run into the problems while making a slightly more complicated table with considerably varied vertical lines and horizontal lines using LaTeX. It may be presumptuous of me to comment
on these debatable matters, but I intend to write down in this article how to solve some of them in the service of your society.
I compiled the table as is given below and the source code is also given below.

source code: table0206.tex
\documentclass[11pt]{article}
\usepackage{hangcaption,array,multirow,hhline}
\parindent=0pt
\begin{document}
\begin{table}[h]
\begin{center}
\begin{sffamily}
\begin{large}
\captionwidth=0.9\textwidth
\newcommand{\captionfonts}{\large\bfseries}
\makeatletter
\long\def\@makecaption#1#2{%
\vskip\abovecaptionskip
\sbox\@tempboxa{{\captionfonts #1: #2}}%
\ifdim \wd\@tempboxa >\hsize
{\captionfonts #1: #2\par}
\else
\hbox to\hsize{\hfil\box\@tempboxa\hfil}%
\fi
\vskip\belowcaptionskip}
\makeatother
\hangcaption{\large\sffamily
\mdseries A Slightly More Complicated Example}\medskip
\newlength{\hheight}
\setlength{\hheight}{32pt}
\newlength{\gheight}
\setlength{\gheight}{20pt}
\newcommand{\bhline}[1]{\noalign{\hrule height #1}}
\newcommand{\bvline}[1]{\vrule width #1}
\renewcommand{\multirowsetup}{\centering}
\renewcommand{\arraystretch}{0.8}
\extrarowheight=15pt
\arraycolsep=0pt
$\hspace{7pt}\overbrace{\hspace{38pt}}^{\mbox{\normalsize65pt}}
\hspace{2pt}\overbrace{\hspace{10pt}}^{\mbox{\normalsize1.6pt}}
\hspace{2pt}
\overbrace{\hspace{38pt}}^{\mbox{\normalsize65pt}}\hspace{2pt}
\overbrace{\hspace{10pt}}^{\mbox{\normalsize1.6pt}}\hspace{2pt}
\overbrace{\hspace{38pt}}^{\mbox{\normalsize65pt}}\hspace{2pt}
\overbrace{\hspace{8pt}}\hspace{2pt}
\overbrace{\hspace{80pt}}^{\mbox{\normalsize100pt}}$\\
$\begin{array}{p{65pt}!{\bvline{1.6pt}}p{65pt}!{\bvline{1.6pt}}
p{65pt}||b{100pt}} \bhline{1.6pt}
\multicolumn{3}{p{198.2pt}||}{\mbox{\centerline{$\backslash
$multicolumn\{3\}\{p\{198.2pt\}\}\{\}}}} &
\multirow{3}{100pt}{\rule{0pt}{\hheight} \mbox{\centerline{$
\backslash$multirow}}}\\[11pt] \hhline{=:=:=#~}
\multicolumn{1}{c!{\bvline{1.6pt}}}{\multirow{2}{65pt}
{\rule{0pt}{\gheight} \mbox{\centerline{$\backslash
$multirow}}}} & \multicolumn{1}{p{65pt}!{\bvline{1.6pt}}}
{\mbox{\centerline{$\backslash$vrule}}} &
\multicolumn{1}{p{65pt}||}{\mbox{\centerline
{$\backslash$vrule}}} & \\[11pt] \cline{2-3}
& \mbox{\centerline{$\backslash$vrule}} &
\mbox{\centerline{$\backslash$vrule}} &
\\[11pt] \hhline{=::=::=#=}
\multicolumn{1}{p{65pt}||}{\mbox{\centerline{
$\backslash$hrule}}} & \multicolumn{1}{p{65pt}||}
{\mbox{\centerline{$\backslash$hrule}}} &
\multicolumn{1}{p{65pt}||}{\mbox{\centerline{
$\backslash$hrule}}} & \multicolumn{1}{p{100pt}}
{\mbox{\centerline{$\backslash$hhline}}}\\[11pt]
\bhline{1.6pt}
\end{array}$ \\
\end{large}
\end{sffamily}
\end{center}
\end{table}
\end{document}
At first, you could draw the vertical lines with varied thickness when you might use \vrule and you could draw the horizontal lines with varied thickness when you might use \hrule. The command lines are given below.
\documentclass[11pt]{article}
\usepackage{array}
\begin{document}
\newcommand{\bhline}[1]{\noalign{\hrule height #1}}
\newcommand{\bvline}[1]{\vrule width #1}
$\begin{array}{p{20pt}!{\bvline{1pt}}p{20pt}} \bhline{1pt}
01 & 02 \\ \bhline{1pt}
\end{array}$
\end{document}Secondly, you could put the double bottom lines on some cells when you might use \hhline. The command lines are given below.
\documentclass[11pt]{article}
\usepackage{array,hhline}
\begin{document}
$\begin{array}{p{20pt}||p{20pt}} \hhline{=#=}
01 & 02 \\ \hhline{=#=}
\end{array}$
\end{document}Thirdly, you could merge some cells in the same row when you might use \multicolumn and you could merge some cells in the same column when you might use \multirow. The command lines are given below.
\documentclass[11pt]{article}
\usepackage{array,multirow}
\begin{document}
$\begin{array}{p{20pt}|p{20pt}} \hline
\multicolumn{2}{p{40.4pt}}{text} \\ \hline
\multirow{2}{20pt}{\mbox{text}} &
\multirow{2}{20pt}{\mbox{text}} \\
& \\ \hline
\end{array}$
\end{document}Finally I am happy to assist you in drawing up a slightly
more complicated table with the varied lines using LaTeX.
The quintessence is to make a few modifications on the first 512 bytes of the boot record copied with dd, which is a common Unix program. For example, therefore, something like a binary editor such as bvi may be
necessary. I also referred to the helpful website, Nobusan's Square, which was written in Japanese, so I'd like to translate and introduce a part of the main points. The URL is given below.
http://www37.tok2.com/home/nobusan/
1. After starting Oracle Solaris 11 installed on the secondary HDD, the first 512 bytes of the boot record need copying. The command lines to confirm the partition table and copy the blocks are given below.
# prtpart /dev/rdsk/c7d0p0 -ldevs
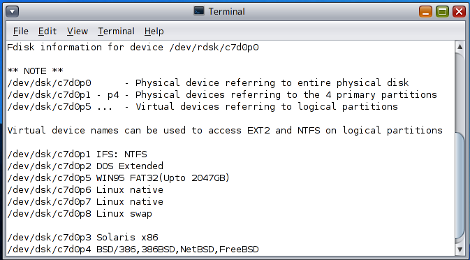 Figure 1 /dev/rdsk/c7d0p0
Figure 1 /dev/rdsk/c7d0p0
# prtpart /dev/rdsk/c9d0p0 -ldevs
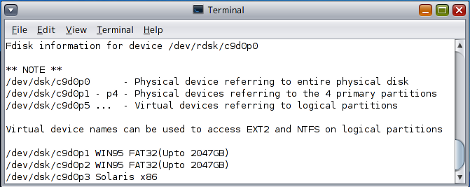 Figure 2 /dev/rdsk/c9d0p0
Figure 2 /dev/rdsk/c9d0p0
# dd if=/dev/dsk/c9d0p3 of=osol.bin bs=512 count=1
2. According to the above website, we modify osol.bin, which is the first 512 bytes of the boot record copied with dd. We substantially make alterations in the first 6 bytes of the file, osol.bin. I specifically say I needed to change the 1st byte EB into B2, the 2nd byte 48 into 81, the 3rd byte 90 into EB,
the 4th byte 00 into 46, which was the number we could obtain when subtracting 2 from the 2nd byte 48, the 5th byte 00 into 90, and the 6th byte 00 into 90. The example to make an amendment is given below.
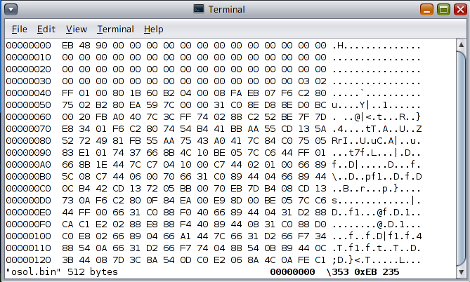
Figure 3 Before Alteration of osol.bin
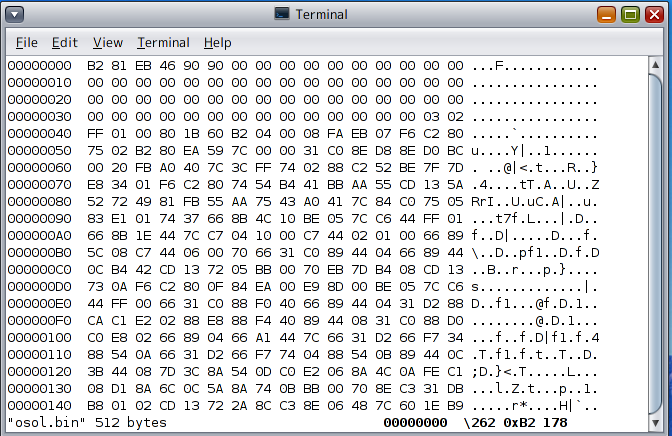
Figure 4 After Alteration of osol.bin
3. We need to rewrite menu.lst in grub not to request the secondary loader on the primary HDD but on the secondary HDD. To put it concretely, I needed to change the line findroot(pool_rpool,1,a) into root (hd1,2,a), which was the partition where I installed Oracle Solaris 11. The example is given below.
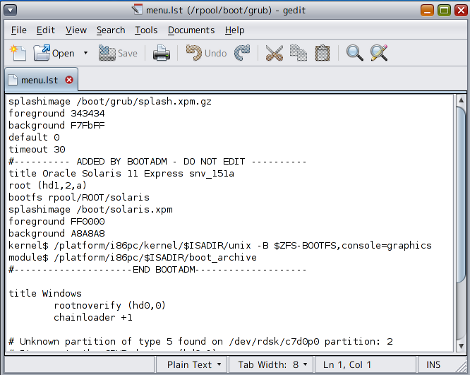
Figure 5 menu.lst
4. We copy osol.bin in the FAT32 partition, and then in the root directory on Windows C drive. Next we use Windows console which requires administrative privilege. The command lines are given below.
> bcdedit /copy {ntldr} /d "OracleSolaris"
> bcdedit /set {GUID} device partition=C:
> bcdedit /set {GUID} path \osol.bin
> bcdedit /displayorder {GUID} /addlast
5. Now we can start Oracle Solaris 11 with the windows boot manager.
Finally I am happy to assist you in starting Oracle Solaris 11 Express build 151a installed on the secondary HDD with the windows boot manager.
At first I will be touching on the correspondence of the Fokker-Planck equation to the stochastic differential equation.![]()
The above stochastic differential equation corresponds to the below Fokker-Planck equation.![]()
We will be solving the above Fokker-Planck equation analytically using the below transformation into the below easy problem.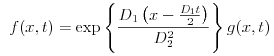
![]()
![]()
We will acquire the below solution to the above Fokker-Planck equation as a result of the above transformation.![]()
We will find the theoretical value of the above Fokker-Planck equation using the above solution.
Well, I will be solving the above Fokker-Planck equation with the finite element method. Let the tent function and f(x,t) be defined as the below equation.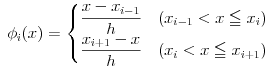
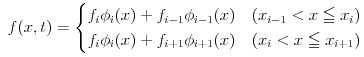
I will also describe the Fokker-Planck equation to use the finite element method.![]()
![]()
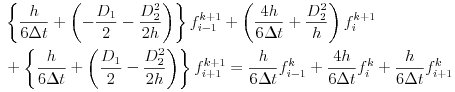
I will represent the above Fokker-Planck equation as the below matrix form.![]()
![]()
![]()
![$$U=\begin{pmatrix} \dfrac{4h}{6\Delta t}+\dfrac{D_2^2}{h} & \dfrac{h}{6\Delta t}+\left(\dfrac{D_1}{2}-\dfrac{D_2^2}{2h}\right) & 0 & \cdots & 0 \\[1.5ex] \dfrac{h}{6\Delta t}+\left(-\dfrac{D_1}{2}-\dfrac{D_2^2}{2h}\right) & \dfrac{4h}{6\Delta t}+\dfrac{D_2^2}{h} & \dfrac{h}{6\Delta t}+\left(\dfrac{D_1}{2}-\dfrac{D_2^2}{2h}\right) & \cdots & 0 \\[1.5ex] 0 & \dfrac{h}{6\Delta t}+\left(-\dfrac{D_1}{2}-\dfrac{D_2^2}{2h}\right) & \dfrac{4h}{6\Delta t}+\dfrac{D_2^2}{h} & \cdots & 0 \\[1.5ex] \vdots & \vdots & \vdots & \ddots & \vdots \\[1.5ex] 0 & 0 & 0 & \cdots & \dfrac{4h}{6\Delta t}+\dfrac{D_2^2}{h} \end{pmatrix}$$](http://paulownia.sakura.ne.jp/materials/learning_journals/archives/eqn56.png)
![$$V=\begin{pmatrix} \dfrac{4h}{6\Delta t} & \dfrac{h}{6\Delta t} & 0 & \cdots & 0 \\[1.5ex] \dfrac{h}{6\Delta t} & \dfrac{4h}{6\Delta t} & \dfrac{h}{6\Delta t} & \cdots & 0 \\[1.5ex] 0 & \dfrac{h}{6\Delta t} & \dfrac{4h}{6\Delta t} & \cdots & 0 \\[1.5ex] \vdots & \vdots & \vdots & \ddots & \vdots \\[1.5ex] 0 & 0 & 0 & \cdots & \dfrac{4h}{6\Delta t} \end{pmatrix}$$](http://paulownia.sakura.ne.jp/materials/learning_journals/archives/eqn57.png)
U and V are the tridiagonal matrices. The example of the finite element method is given below.
source code: FokkerPlanck.java
import java.awt.*;
import java.awt.event.*;
import java.text.DecimalFormat;
import java.applet.Applet;
import javax.swing.JLabel;
import javax.swing.JTextField;
public class FokkerPlanck extends Applet implements ActionListener{
// variable set
private static final long serialVersionUID = 9129736202608299398L;
public static double d1 = 2;
public static double d2 = 3;
public static double t = 1;
public static double h = 0.055;
public static double dt = 0.25;
public static double[] s1 = new double[1000];
public static double[] s2 = new double[1000];
public static double[] s3 = new double[1000];
public static double[] s4 = new double[1000];
public static int[][] xxxx = new int [56][1002];
public static int[][] yyyy = new int [56][1002];
public static int[] xxxx1 = new int [1002];
public static int[] yyyy1 = new int [1002];
public static int[] xxxx2 = new int [1000];
public static int[] yyyy2 = new int [1000];
public static int[] xxxx3 = new int [1000];
public static int[] yyyy3 = new int [1000];
public static double[][] MatrixL = new double[1000][1000];
public static double[][] MatrixU = new double[1000][1000];
public static double[][] Matrix01 = new double[1000][1000];
public static double[][] Matrix02 = new double[1000][1000];
public static double[][] Matrix03 = new double[1000][1000];
public static double[][] vector01 = new double[57][1000];
public static double[][] vector02 = new double[56][1000];
public static double[][] vector03 = new double[56][1000];
JTextField yx = new JTextField("2.0");
JTextField yn = new JTextField("3.0");
JTextField yr = new JTextField("0.055");
JLabel label1 = new JLabel("The Example of The Finite Element Method",JLabel.CENTER);
JLabel label2 = new JLabel("<html><body><font size=3>The Drift Coefficient (0<D<sub>1</sub>≤10<sup>8</sup>)</font></body></html>",JLabel.CENTER);
JLabel label3 = new JLabel("<html><body><font size=3>The Diffusion Coefficient (0<D<sub>2</sub>≤10<sup>8</sup>)</font></body></html>",JLabel.CENTER);
JLabel label4 = new JLabel("<html><body><font size=3>The Interval between x<sub>i</sub> and x<sub>i+1</sub></font></body></html>", JLabel.CENTER);
public void init(){
label1.setPreferredSize(new Dimension(416,24));
label1.setFont(new Font("Serif",Font.BOLD,14));
add(label1);
label2.setPreferredSize(new Dimension(260,23));
label2.setFont(new Font("Serif",Font.BOLD,11));
add(label2);
yx.setPreferredSize(new Dimension(80,23));
add(yx);
label3.setPreferredSize(new Dimension(260,23));
label3.setFont(new Font("Serif",Font.BOLD,11));
add(label3);
yn.setPreferredSize(new Dimension(80,23));
add(yn);
label4.setPreferredSize(new Dimension(260,23));
label4.setFont(new Font("Serif",Font.BOLD,11));
add(label4);
yr.setPreferredSize(new Dimension(80,23));
add(yr);
yx.addActionListener(this);
yn.addActionListener(this);
yr.addActionListener(this);
}
public void actionPerformed(ActionEvent e){
if(e.getSource()==yx){
d1=Double.valueOf(yx.getText()).doubleValue();
if(d1 <= 0 || d1 > Math.pow(10.0,8)){
d1 = 2.0;
}
}
if(e.getSource()==yn){
d2 = Double.valueOf(yn.getText()).
doubleValue();
if(d2 <= 0 || d2 > Math.pow(10.0,8)){
d2 = 3.0;
}
}
if(e.getSource()==yr){h = Double.valueOf
(yr.getText()).doubleValue();
if(h <= 0 || h > Math.pow(10.0,8)){h = 0.055;}
}
yx.setText(""+d1);
yn.setText(""+d2);
yr.setText(""+h);
repaint();
}
public void paint(Graphics g){
for(int i=0;i<1000;i++){
s1[i]=(i*0.05-10)*d2/3;
}
for(int i=0;i<1000;i++){
s2[i]=function(d1,d2,s1[i],1);
}
for(int i=0;i<1000;i++){
s3[i]=function(d1,d2,s1[i],6);
}
for(int i=0;i<1000;i++){
s4[i]=function(d1,d2,s1[i],14);
}
Matrix01[0][0]=4*h/(6*dt)+Math.pow(d2,2)/h;
Matrix01[0][1]=h/(6*dt)+d1/2-Math.pow(d2,2)/(2*h);
for(int i=1;i<999;i++){
Matrix01[i][i-1]=h/(6*dt)-d1/2-Math.pow(d2,2)/(2*h);
Matrix01[i][i]=4*h/(6*dt)+Math.pow(d2,2)/h;
Matrix01[i][i+1]=h/(6*dt)+d1/2-Math.pow(d2,2)/(2*h);
}
Matrix01[999][998]=h/(6*dt)-d1/2-Math.pow(d2,2)/(2*h);
Matrix01[999][999]=4*h/(6*dt)+Math.pow(d2,2)/h;
Matrix02[0][0]=4*h/(6*dt);
Matrix02[0][1]=h/(6*dt);
for(int i=1;i<999;i++){
Matrix02[i][i-1]=h/(6*dt);
Matrix02[i][i]=4*h/(6*dt);
Matrix02[i][i+1]=h/(6*dt);
}
Matrix02[999][998]=h/(6*dt);
Matrix02[999][999]=4*h/(6*dt);
vector01[0][0]=Matrix02[0][0]*s2[0]+Matrix02[0][1]*s2[1];
for(int i=1;i<999;i++){
vector01[0][i]=Matrix02[i][i-1]*s2[i-1]+Matrix02[i][i]*s2[i]+Matrix02[i][i+1]*s2[i+1];
}
vector01[0][999]=Matrix02[999][998]*s2[998]+Matrix02[999][999]*s2[999];
for(int i=0;i<1000;i++){
for(int j=0;j<1000;j++){
MatrixU[i][j]=Matrix01[i][j];
}
}
for(int i=1;i<1000;i++){
MatrixU[i][i]=Matrix01[i][i]-MatrixU[i-1][i]*Matrix01[i][i-1]/MatrixU[i-1][i-1];
}
MatrixL[0][0]=1;
for(int i=1;i<1000;i++){
MatrixL[i][i-1]=Matrix01[i][i-1]/MatrixU[i-1][i-1];
MatrixL[i][i]=1;
}
for(int k=0;k<56;k++){
vector02[k][0]=vector01[k][0];
for(int i=1;i<1000;i++){
vector02[k][i]=vector01[k][i]-MatrixL[i][i-1]*vector02[k][i-1];
}
vector03[k][999]=vector02[k][999]/MatrixU[999][999];
for(int i=998;i>=0;i--){
vector03[k][i]=(vector02[k][i]-MatrixU[i][i+1]*vector03[k][i+1])/MatrixU[i][i];
}
vector01[k+1][0]=Matrix02[0][0]*vector03[k][0]+Matrix02[0][1]*vector03[k][1];
for(int i=1;i<999;i++){
vector01[k+1][i]=Matrix02[i][i-1]*vector03[k][i-1]+Matrix02[i][i]*vector03[k][i]+Matrix02[i][i+1]*vector03[k][i+1];
}
vector01[k+1][999]=Matrix02[999][998]*vector03[k][998]+Matrix02[999][999]*vector03[k][999];
}
double minss1 = s1[0];
double maxss1 = s1[0];
for(int i=0;i<1000;i++){
if(s1[i]>maxss1){
maxss1 = s1[i];
}
}
for(int i=0;i<1000;i++){
if(s1[i]<minss1){
minss1 = s1[i];
}
}
for(int j=0;j<56;j++){
for(int i=0;i<1000;i++){
xxxx[j][i] = (int)(i*351/999)+33;
yyyy[j][i] = 295-(int)((vector03[j][i])*176/0.2);
}
xxxx[j][1000]=33;
xxxx[j][1001]=387;
yyyy[j][1000]=299;
yyyy[j][1001]=299;
}
for(int i=0;i<1000;i++){
xxxx1[i] = (int)(i*351/999)+33;
yyyy1[i] = 295-(int)((s2[i])*176/0.2);
}
xxxx1[1000]=33;
xxxx1[1001]=387;
yyyy1[1000]=299;
yyyy1[1001]=299;
for(int i=0;i<1000;i++){
xxxx2[i] = (int)(i*351/999)+33;
yyyy2[i] = 295-(int)((s3[i])*176/0.2);
}
for(int i=0;i<1000;i++){
xxxx3[i] = (int)(i*351/999)+33;
yyyy3[i] = 295-(int)((s4[i])*176/0.2);
}
Graphics2D g2 = (Graphics2D)g;
GradientPaint gp1 = new GradientPaint(0, 0, new Color(154,181,228), 0,470,new Color(225,232,245), true);
g2.setPaint(gp1);
g2.fillRect(0,0,416,328);
super.paint(g);
GradientPaint gp2 = new GradientPaint(0, 33, new Color(225,232,245), 0,351,new Color(154,181,228), true);
g2.setPaint(gp2);
g2.fillRect(33,123,354,176);
GradientPaint gp4 = new GradientPaint(33,227, new Color(192,88,77), 33,418,new Color(160,82,45), true);
g2.setPaint(gp4);
for(int k=0;k<2;k++){
for(int i=0;i<12;i++){
g2.setPaint(gp4);
g2.fillPolygon(xxxx1,yyyy1,1001);
}
g2.setPaint(gp2);
g2.fillRect(33,123,354,176);
for(int i=0;i<56;i+=4){
for(int j=0;j<12;j++){
g2.setPaint(gp4);
g2.fillPolygon(xxxx[i],yyyy[i],1001);
}
g2.setPaint(gp2);
g2.fillRect(33,123,354,176);
}
g2.setPaint(gp4);
g2.fillPolygon(xxxx[55],yyyy[55],1001);
g2.setPaint(gp2);
g2.fillRect(33,123,354,176);
}
for(int i=0;i<1000;i++){
g2.setColor (new Color(0,0,0));
g2.fillOval(xxxx1[i], yyyy1[i], 3, 3);
}
for(int i=0;i<1000;i++){
g2.fillOval(xxxx2[i], yyyy2[i], 3, 3);
}
for(int i=0;i<1000;i++){
g2.fillOval(xxxx3[i], yyyy3[i], 3, 3);
}
for(int j=0;j<1000;j++){
g2.setPaint(gp4);
g2.fillOval(xxxx[23][j], yyyy[23][j], 3, 3);
g2.fillOval(xxxx[55][j], yyyy[55][j], 3, 3);
}
GradientPaint gp3 = new GradientPaint(33, 227, new Color(79,129,189), 33,418,new Color(65,105, 225), true);
g2.setPaint(gp3);
DecimalFormat df0 = new DecimalFormat("0.00");
DecimalFormat df1 = new DecimalFormat("0.000");
for(int i=0;i<5;i++){
g2.setFont(new Font ("Serif",Font.BOLD,12));
g2.setColor (new Color(0,0,0));
String subx = df1.format((maxss1-minss1)/4*i+minss1);
g2.drawString(subx,14+88*i,313);
}
for(int i=0;i<3;i++){
g2.setFont(new Font ("Serif",Font.BOLD,12));
g2.setColor (new Color(0,0,0));
String suby = df0.format(0.1*i);
g2.drawString(suby,3,299-85*i);
}
g2.setFont(new Font ("Serif",Font.BOLD,12));
g2.setColor (new Color(0,0,0));
g2.drawString("n = 1000",250,152);
g2.setColor (new Color(79,129,189));
BasicStroke BoldLine = new BasicStroke(2.8f);
g2.setStroke(BoldLine);
g2.drawLine(250,182,320,162);
g2.setColor (new Color(0,0,0));
g2.drawString("The Analytic Solution",250,182);
g2.setPaint(gp4);
g2.drawLine(250,212,320,192);
g2.setColor (new Color(0,0,0));
g2.drawString("The FEM Solution",250,212);
g2.drawLine(250,222,320,222);
g2.setColor (new Color(0,0,0));
g2.drawString("The Initial Value",250,242);
g2.drawString("f",15,115);
g2.drawString("x",340,313);
}
public static double function(double d1, double d2, double x, double t){
return 1/Math.pow(Math.PI*2*Math.pow(d2,2)*t,0.5)*Math.exp(-Math.pow((x-d1*t),2)/(2*Math.pow(d2,2)*t));
}
}
In conclusion the difference between the analytic solution and the solution with the finite element method seems to depend on the form of the tent function and other parameters and still more improvement seems to be necessary. There is a great deal of room for improvement.
Finally I am happy to assist you in coding and solving the Fokker-Planck equation with the finite element method in JAVA.
At the beginning of this article I explicitly say the data set necessary to estimate the logistic function was generated from the below equations.![]()
![]()
![]()
The logistic function was the solution acquired by solving the below differential equation with the separation of variables.![]()
I tentatively interpret r as the growth rate and K as the carrying capacity. The above differential equation was different from the below form I initially thought. I read up on the forms, running my eyes through en.wikipedia. org, fr.wikipedia.org, and de.wikipedia.org. The above
form was adopted in American and French Wikipedia and the below form was adopted in German Wikipedia as of October 5, 2010.![]()
After that I used the Gauss-Newton algorithm to estimate the logistic function. The algorithm is given below.![]()
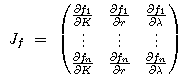
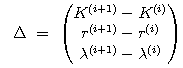
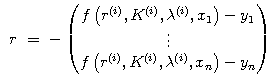
Then I used the LU decomposition of JfTJf and didn't accordingly find the inverse matrix of JfTJf to economize on computational resources. The example of the LU decomposition is given below.![]()
I also used the method of forward substitution to find b and the method of back substitution to find Δ.![]()
![]()
The convergence of r, K, and λ to the theoretical value is given below.
source code: GaussNewton.java
import java.awt.*;
import java.awt.event.*;
import java.text.DecimalFormat;
import java.applet.Applet;
import javax.swing.JLabel;
import javax.swing.JTextField;
public class GaussNewton extends Applet implements ActionListener{
// variable set
private static final long serialVersionUID = -1173026208646241820L;
public static double r = 1.0;
public static double k = 1.0;
public static double c = 1.0;
public static double[] s1 = new double[1000];
public static double[] s2 = new double[1000];
public static double[] s3 = new double[1000];
public static double[] se1 = new double[1000];
public static double[] k0 = new double[1000];
public static double[] r0 = new double[1000];
public static double[] c0 = new double[1000];
public static double[] dk = new double[1000];
public static double[] dr = new double[1000];
public static double[] dc = new double[1000];
public static double[] k3 = new double [3];
public static double[] k4 = new double [3];
public static double[] r3 = new double [3];
public static int[] xxxx = new int [1000];
public static int[] yyyy = new int [1000];
public static int[] xxxx1 = new int [1000];
public static int[] yyyy1 = new int [1000];
public static double[][] Matrix = new double[3][3];
public static double[][] MatrixL = new double[3][3];
public static double[][] MatrixU = new double[3][3];
public static double[][] MatrixU1 = new double[3][3];
JTextField yx = new JTextField("1.0");
JTextField yn = new JTextField("1.0");
JTextField yr = new JTextField("1.0");
JLabel label1 = new JLabel("The Example of The Gauss-Newton algorithm",JLabel.CENTER);
JLabel label2 = new JLabel("<html><body><font size=3>The Growth Rate (0<r≤10<sup>8</sup>)</font></body></html>",JLabel.CENTER);
JLabel label3 = new JLabel("<html><body><font size=3>The Carrying Capacity (0<K≤10<sup>8</sup>)</font></body></html>",JLabel.CENTER);
JLabel label4 = new JLabel("<html><body><font size=3>The Integration Constant (-10<sup>8</sup><λ≤10<sup>8</sup>)</font></body></html>", JLabel.CENTER);
public void init(){
label1.setPreferredSize(new Dimension(416,24));
label1.setFont(new Font("Serif",Font.BOLD,14));
add(label1);
label2.setPreferredSize(new Dimension(260,23));
label2.setFont(new Font("Serif",Font.BOLD,11));
add(label2);
yx.setPreferredSize(new Dimension(80,23));
add(yx);
label3.setPreferredSize(new Dimension(260,23));
label3.setFont(new Font("Serif",Font.BOLD,11));
add(label3);
yn.setPreferredSize(new Dimension(80,23));
add(yn);
label4.setPreferredSize(new Dimension(260,23));
label4.setFont(new Font("Serif",Font.BOLD,11));
add(label4);
yr.setPreferredSize(new Dimension(80,23));
add(yr);
yx.addActionListener(this);
yn.addActionListener(this);
yr.addActionListener(this);
}
public void actionPerformed(ActionEvent e){
if(e.getSource()==yx){
r=Double.valueOf(yx.getText()).doubleValue();
if(r <= 0 || r > Math.pow(10.0,8)){
r = 1.0;
}
}
if(e.getSource()==yn){
k = Double.valueOf(yn.getText()).doubleValue();
if(k <= 0 || k > Math.pow(10.0,8)){
k = 1.0;
}
}
if(e.getSource()==yr){c = Double.valueOf(yr.getText())
.doubleValue();
if(c < -Math.pow(10.0,8) || c > Math.pow(10.0,8)){c = 1.0;}
}
yx.setText(""+r);
yn.setText(""+k);
yr.setText(""+c);
repaint();
}
public void paint(Graphics g){
s1[0] = (Math.log(Math.abs(c))+Math.log(k)-Math.log(999))/r;
s1[999] = (Math.log(Math.abs(c))+Math.log(k)+Math.log(999))/r;
double aa=(s1[999]-s1[0])/999;
s2[0]=function(k,r,c,s1[0]);
s2[999]=function(k,r,c,s1[999]);
for(int i=1;i<999;i++){
s1[i]=s1[i-1]+aa;
}
for(int i=1;i<999;i++){
s2[i]=function(k,r,c,s1[i]);
}
for(int i=0;i<1000;i++){
se1[i]=normal.sampleNormal(0,k/50);
}
for(int i=0;i<1000;i++){
s3[i]=s2[i]+se1[i];
}
for(int i=0;i<3;i++){
for(int j=0;j<3;j++){
Matrix[i][j]=0;
}
}
k0[0]=k;
r0[0]=r;
c0[0]=c;
for(int h=0;h<999;h++){
for(int i=0;i<1000;i++){
dk[i] = (1+c0[h]*k0[h]*Math.exp(r0[h]*(-s1[i]))-k0[h]*c0[h]*Math.exp(r0[h]*(-s1[i])))/Math.pow(1+c0[h]*k0[h]*Math.exp(r0[h]*(-s1[i])),2);
dr[i] = -Math.pow(k0[h],2)*(-s1[i])*c0[h]*Math.exp(r0[h]*(-s1[i]))/Math.pow(1+c0[h]*k0[h]*Math.exp(r0[h]*(-s1[i])),2);
dc[i] = -Math.pow(k0[h],2)*Math.exp(r0[h]*(-s1[i]))/Math.pow(1+c0[h]*k0[h]*Math.exp(r0[h]*(-s1[i])),2);
Matrix[0][0]=Matrix[0][0]+Math.pow(dk[i],2);
Matrix[0][1]=Matrix[0][1]+dk[i]*dr[i];
Matrix[0][2]=Matrix[0][2]+dk[i]*dc[i];
Matrix[1][0]=Matrix[1][0]+dr[i]*dk[i];
Matrix[1][1]=Matrix[1][1]+Math.pow(dr[i],2);
Matrix[1][2]=Matrix[1][2]+dr[i]*dc[i];
Matrix[2][0]=Matrix[2][0]+dc[i]*dk[i];
Matrix[2][1]=Matrix[2][1]+dc[i]*dr[i];
Matrix[2][2]=Matrix[2][2]+Math.pow(dc[i],2);
}
MatrixU[0][0]=Matrix[0][0];
MatrixU[0][1]=Matrix[0][1];
MatrixU[0][2]=Matrix[0][2];
MatrixU[1][0]=0;
MatrixU[1][1]=Matrix[1][1]-Matrix[0][1]*Matrix[1][0]/Matrix[0][0];
MatrixU[1][2]=Matrix[1][2]-Matrix[0][2]*Matrix[1][0]/Matrix[0][0];
MatrixU[2][0]=0;
MatrixU[2][1]=Matrix[2][1]-Matrix[0][1]*Matrix[2][0]/Matrix[0][0];
MatrixU[2][2]=Matrix[2][2]-Matrix[0][2]*Matrix[2][0]/Matrix[0][0];
MatrixU1[2][0]=0;
MatrixU1[2][1]=0;
MatrixU1[2][2]=MatrixU[2][2]-MatrixU[1][2]*MatrixU[2][1]/MatrixU[1][1];
MatrixL[0][0]=1;
MatrixL[0][1]=0;
MatrixL[0][2]=0;
MatrixL[1][0]=Matrix[1][0]/Matrix[0][0];
MatrixL[1][1]=1;
MatrixL[1][2]=0;
MatrixL[2][0]=Matrix[2][0]/Matrix[0][0];
MatrixL[2][1]=MatrixU[2][1]/MatrixU[1][1];
MatrixL[2][2]=1;
r3[0]=0;
r3[1]=0;
r3[2]=0;
for(int i=0;i<1000;i++){
r3[0]=r3[0]-dk[i]*(k0[h]/(1+c0[h]*k0[h]*Math.exp(r0[h]*(-s1[i])))-s3[i]);
r3[1]=r3[1]-dr[i]*(k0[h]/(1+c0[h]*k0[h]*Math.exp(r0[h]*(-s1[i])))-s3[i]);
r3[2]=r3[2]-dc[i]*(k0[h]/(1+c0[h]*k0[h]*Math.exp(r0[h]*(-s1[i])))-s3[i]);
}
k4[0]=r3[0];
k4[1]=r3[1]-MatrixL[1][0]*k4[0];
k4[2]=r3[2]-MatrixL[2][0]*k4[0]-MatrixL[2][1]*k4[1];
k3[2]=k4[2]/MatrixU1[2][2];
k3[1]=(k4[1]-MatrixU[1][2]*k3[2])/MatrixU[1][1];
k3[0]=(k4[0]-MatrixU[0][1]*k3[1]-MatrixU[0][2]*k3[2])/MatrixU[0][0];
k0[h+1]=k0[h]+k3[0];
r0[h+1]=r0[h]+k3[1];
c0[h+1]=c0[h]+k3[2];
}
double minss3 = s3[0];
double maxss3 = s3[0];
if(c>=0){
for(int i=0;i<1000;i++){
if(s3[i]>maxss3){
maxss3 = s3[i];
}
}
for(int i=0;i<1000;i++){
if(s3[i]<minss3){
minss3 = s3[i];
}
}
}
if(c<0){
for(int i=525;i<1000;i++){
if(s3[i]>maxss3){
maxss3 = s3[i];
}
}
for(int i=0;i<475;i++){
if(s3[i]<minss3){
minss3 = s3[i];
}
}
}
for(int i=0;i<1000;i++){
xxxx[i] = (int)(i*351/999)+33;
yyyy[i] = 474-(int)((s3[i]-minss3)*351/(maxss3-minss3)*345/351+6);
}
for(int i=0;i<1000;i++){
xxxx1[i] = (int)(i*351/999)+33;
yyyy1[i] = 474-(int)((function(k0[999],r0[999],c0[999],s1[i])-minss3)*351/(maxss3-minss3)*345/351+6);
}
Graphics2D g2 = (Graphics2D)g;
GradientPaint gp1 = new GradientPaint(0, 0, new Color(154,181,228), 0,470,new Color(225,232,245), true);
g2.setPaint(gp1);
g2.fillRect(0,0,416,503);
super.paint(g);
GradientPaint gp2 = new GradientPaint(0, 33, new Color(225,232,245), 0,351,new Color(154,181,228), true);
g2.setPaint(gp2);
g2.fillRect(33,123,354,351);
GradientPaint gp4 = new GradientPaint(33, 227, new Color(192,88,77), 33,418,new Color(160,82,45), true);
g2.setPaint(gp4);
if(c>=0){
for (int i=0;i<1000;i++){
g2.fillOval(xxxx[i], yyyy[i], 4, 4);
}
}
if(c<0){
for (int i=0;i<475;i++){
g2.fillOval(xxxx[i], yyyy[i], 4, 4);
}
for (int i=525;i<1000;i++){
g2.fillOval(xxxx[i], yyyy[i], 4, 4);
}
}
GradientPaint gp3 = new GradientPaint(33, 227, new Color(79,129,189), 33,418,new Color(65,105,225), true);
g2.setPaint(gp3);
BasicStroke BoldLine = new BasicStroke(2.8f);
g2.setStroke(BoldLine);
if(c>=0){
for (int i=1;i<1000;i++){
g2.drawLine(xxxx1[i-1], yyyy1[i-1], xxxx1[i], yyyy1[i]);
}
}
if(c<0){
for (int i=1;i<475;i++){
g2.drawLine(xxxx1[i-1], yyyy1[i-1], xxxx1[i], yyyy1[i]);
}
for (int i=526;i<1000;i++){
g2.drawLine(xxxx1[i-1], yyyy1[i-1], xxxx1[i], yyyy1[i]);
}
}
DecimalFormat df0 = new DecimalFormat("0.00");
DecimalFormat df1 = new DecimalFormat("0.000");
DecimalFormat df2 = new DecimalFormat("0.000000");
for(int i=0;i<5;i++){
g2.setFont(new Font ("Serif",Font.BOLD,12));
g2.setColor (new Color(0,0,0));
String subx = df1.format(s1[0+249*i]);
g2.drawString(subx,14+88*i,488);
}
for(int i=1;i<5;i++){
g2.setFont(new Font ("Serif",Font.BOLD,12));
g2.setColor (new Color(0,0,0));
String suby = df0.format(maxss3/4*i);
g2.drawString(suby,3,484-87*i);
}
g2.setFont(new Font ("Serif",Font.BOLD,12));
g2.setColor (new Color(0,0,0));
g2.drawString("n = 1000",280,367);
g2.drawString("r",280,387);
g2.drawString("*",290,386);
g2.drawString(" =",293,387);
g2.drawString(df2.format(r0[999]),315,387);
g2.drawString("k",280,407);
g2.drawString("*",290,407);
g2.drawString(" =",293,407);
g2.drawString(df2.format(k0[999]),315,407);
g2.drawString("c",280,427);
g2.drawString("*",290,427);
g2.drawString(" =",293,427);
g2.drawString(df2.format(c0[999]),315,427);
g2.drawString("y",15,115);
g2.drawString("x",340,488);
}
public static double function(double k,double r,double c,
double x){
return k/(1+c*k*Math.exp(r*(-x)));
}
}
source code: normal.java
import java.util.*;
public class normal {
private static Random rnd = new Random(Calendar.getInstance().getTimeInMillis()+Thread.currentThread().getId());
private static double u;
public static double sampleNormal(double e0, double e1) {
double e2;
e2=Math.pow(e1,(0.5));
u=e2*rnd.nextGaussian()+e0;
return u;
}
}
In conclusion the estimates of the parameters was susceptible to influences of the initial values of the
parameters under the Gauss-Newton algorithm. r and K could converge on the theoretical values when the initial values of the parameters was set to half of the theoretical values but λ couldn't converge under the same condition where a number of times of iteration was between 1000 and 10000. The form of f(xi) was the normal logistic curve when the value of λ was positive and the different curve when the value of λ was negative.
Finally I am happy to assist you in coding and
estimating the logistic function with the Gauss-
Newton algorithm in JAVA.
This article is principally indebted to the works of Yoshiyuki Wakui, who is Japanese researcher in mathematics, in the same way as Part 1. I experimentally introduced the bimodal distribution to the research and
I'd very much appreciate the useful descriptions.
First I also tentatively outline the situation we were put in. Someone who was busy with his work generated two sorts of normal random numbers with a computer. One followed N(-0.7,1) and the other followed N(0.7,1).
As his phone abruptly rang, he had to deal with something urgent. After a while he realized he clean forgot the variances of the normal random variables and barely remembered the population means of the data sets
and the distributions of the data sets. Unfortunately, he needed to generate the additional normal random numbers which followed the almost same normal distributions.
1. The Data Sets
The data sets he generated at that time is given below.
| n | 1 | 2 | 3 | 4 | 5 |
| yA | -2.18 | -1.19 | -0.74 | -1.2 | -2.53 |
| n | 6 | 7 | 8 | 9 | 10 |
| yA | -0.5 | 0.09 | 0.31 | -1.71 | -0.67 |
| n | 11 | 12 | 13 | 14 | 15 |
| yB | 0.59 | 0.13 | 1.22 | 0.45 | -0.22 |
| n | 16 | 17 | 18 | 19 | 20 |
| yB | 0.15 | 1.5 | 1.06 | 1.32 | 1.88 |
The unstratified sample mean is about -0.11 and the unstratified and unbiased sample variance is about 1.52. Number 1-10, yA are actually generated from the normal distribution N(-0.7,1) and number 11-20, yB are generated from the normal distribution N(0.7,1). He clean forgot the population variances of the data sets but fortunately remembered the population means of the data sets, yA and yB. That is to say we pretend to forget the population variances of the data sets, yA and yB.
2. The Estimation of The Prior Distribution
I supposed that the population mean μ of the random variables y followed the bimodal distribution, that the
population mean μA of the random variables yA and
the population mean μB of the random variables yB
followed the different normal distributions, that the hyperparameter, which was the probability that the population mean of the 10 random variables yA of the 20 random variables y took the population mean μA, was set to 0.5, that the hyperparameter, which was
the probability that the population mean of the 10 random variables yB of the 20 random variables y took the population mean μB, was set to 0.5, that the population mean μA was -0.7, that the population mean μB was 0.7, that the population
variance of μA and μB was in proportion to the
population variance σ2 of the random variables y, and that the population variance σ2 of the random variables y followed the inverse gamma distribution. The example of the prior distribution is given below.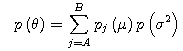
We substitute pA(μ), B(μ), and p(σ2) in the above equation to find the prior distribution.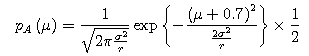
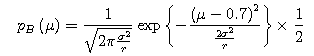
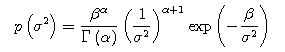
We also substitute the parameters for both E(σ2)
and Var(σ2) in the below equations to find the
value of both α and β.![]()
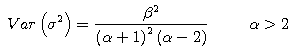
source code: PriorMultiModal.java
import java.awt.*;
import java.awt.event.*;
import java.applet.Applet;
import javax.swing.JLabel;
import javax.swing.JTextField;
public class PriorMultiModal extends Applet implements ActionListener{
// variable set
private static final long serialVersionUID = -3846703423854379608L;
final static int StartingX=50,StartingY=527;
final static String[] rulerX = {"",""," -1.6",""," -0.8", ""," 0",""," 0.8",""," 1.6",""};
final static String[] rulerY = {"",""," 0.2",""," 0.6", ""," 1.0",""," 1.4",""," 1.8",""};
final static String[] rulerZ = {"","","","",""," 0","","","","","","","",""};
final int EndingX=StartingX+transformation(120,120,120).x;
final int EndingY=StartingY+transformation(120,-120,-120).y;
public int[] SmallestInnerPart=new int[EndingX+1];
public int[] LargestInnerPart=new int[EndingX+1];
public static double exp = 1.0;
public static double var = 1.0;
public static double ratio = 3.0;
JTextField yx = new JTextField("1.0");
JTextField yn = new JTextField("1.0");
JTextField yr = new JTextField("3.0");
JLabel label1 = new JLabel("The Prior Distribution",JLabel.CENTER);
JLabel label2 = new JLabel("<html><body><font size=3>The Expectation of σ<sup>2</sup> (0<E(σ<sup>2</sup>)≤2.0)</font></body></html>", JLabel.CENTER);
JLabel label3 = new JLabel("<html><body><font size=3>The Variance of σ<sup>2</sup> (0<Var(σ<sup>2</sup>)≤10<sup>8</sup>)</font></body></html>", JLabel.CENTER);
JLabel label4 = new JLabel("<html><body><font size=3>The Ratio of σ<sup>2</sup> to Var(μ<sub>j</sub>) (0<r≤10<sup>8</sup>)</font></body></html>", JLabel.CENTER);
public void init(){
label1.setPreferredSize(new Dimension(400,24));
label1.setFont(new Font("Serif",Font.BOLD,15));
add(label1);
label2.setPreferredSize(new Dimension(260,23));
label2.setFont(new Font("Serif",Font.BOLD,11));
add(label2);
yx.setPreferredSize(new Dimension(120,23));
add(yx);
label3.setPreferredSize(new Dimension(260,23));
label3.setFont(new Font("Serif",Font.BOLD,11));
add(label3);
yn.setPreferredSize(new Dimension(120,23));
add(yn);
label4.setPreferredSize(new Dimension(260,23));
label4.setFont(new Font("Serif",Font.BOLD,11));
add(label4);
yr.setPreferredSize(new Dimension(120,23));
add(yr);
yx.addActionListener(this);
yn.addActionListener(this);
yr.addActionListener(this);
}
public void actionPerformed(ActionEvent e){
if(e.getSource()==yx){exp = Double.valueOf(yx.getText()).doubleValue();
if(exp <= 0 || exp > 2.0){exp=1.0;
}
}
if(e.getSource()==yn){var = Double.valueOf(yn.getText()).doubleValue();
if(var <= 0 || var > Math.pow(10.0,8))
{var=1.0;
}
}
if(e.getSource()==yr){ratio = Double.valueOf(yr.getText()).doubleValue();
if(ratio <= 0 || ratio > Math.pow(10.0,8))
{ratio=3.0;
}
}
yx.setText(""+exp);
yn.setText(""+var);
yr.setText(""+ratio);
repaint();
}
public void paint(Graphics g){
Point dot,dot1,dot2,dot3,dot4,dot5,dot6;
Graphics2D g2 = (Graphics2D)g;
GradientPaint gp1 = new GradientPaint(0, 0, new Color(154,181,228), 0,470,new Color(225,232,245), true);
g2.setPaint(gp1);
g2.fillRect(0,0,460,447);
super.paint(g);
// x axis
g.setColor(new Color(128,128,128));
dot1=transformation(-120,-120,0);
dot2=transformation(120,-120,0);
g.drawLine(dot1.x,dot1.y,dot2.x,dot2.y);
for(int i=0;i<21;i++){
dot1=transformation((120/10*i-120),-120,0);
if(i % 4==0){
dot2=transformation((120/10*i-120),(-120-10),0);
g.setColor(new Color(128,128,128));
g.drawLine(dot1.x,dot1.y,dot2.x,dot2.y);
g2.setFont(new Font ("SanSerif",Font.PLAIN,12));
g.drawString(rulerX[i/2],dot2.x-48,dot2.y+15);
if(i==8)
g.drawString("μ",dot2.x+28,dot2.y+30);
}
}
// y axis
g.setColor(new Color(128,128,128));
dot1=transformation(-120,-120,0);
dot2=transformation(-120,120,0);
dot3=transformation(-120,120,0);
dot4=transformation(-120,120,210);
dot5=transformation(120,-120,0);
dot6=transformation(120,120,0);
g.drawLine(dot1.x,dot1.y,dot2.x,dot2.y);
g.drawLine(dot3.x,dot3.y,dot4.x,dot4.y);
g.drawLine(dot5.x,dot5.y,dot6.x,dot6.y);
for(int i=0;i<210;i=i+1){
dot3=transformation(-119,120,i);
dot4=transformation(120,120,i);
g.setColor(new Color(154,181,228));
g.drawLine(dot3.x,dot3.y,dot4.x,dot4.y);
}
g.setColor(new Color(128,128,128));
for(int i=3;i<10;i++){
dot3=transformation(-120,120,(12/4*(i+3)-15)*10);
dot4=transformation(120,120,(12/4*(i+3)-15)*10);
g.drawLine(dot3.x,dot3.y,dot4.x,dot4.y);
}
for(int i=0;i<21;i++){
dot1=transformation(120,(12*i-120),0);
if(i % 4==0){
dot2=transformation((12+1)*10,(12*i-120),0);
g.setColor(new Color(128,128,128));
g.drawLine(dot1.x,dot1.y,dot2.x,dot2.y);
g.setFont(new Font ("SanSerif",Font.PLAIN,12));
g.drawString(rulerY[i/2],dot2.x-10,dot2.y+13);
if(i==8) g.drawString("σ",dot2.x+38,dot2.y+16);
g2.setFont(new Font ("SanSerif",Font.PLAIN,8));
if(i==8) g.drawString("2",dot2.x+47,dot2.y+9);
}
}
// z axis
g.setColor(new Color(128,128,128));
dot1=transformation(-120,-120,0);
dot2=transformation(-120,-120,210);
dot3=transformation(-120,119,210);
dot4=transformation(-120,119,0);
g.drawLine(dot1.x,dot1.y,dot2.x,dot2.y);
g.drawLine(dot2.x,dot2.y,dot3.x,dot3.y);
g.drawLine(dot3.x,dot3.y,dot4.x,dot4.y);
for(int i=0;i<240;i=i+1){
g.setColor(new Color(154,181,228));
dot5=transformation(-120,(-119+i),210);
dot6=transformation(-120,(-119+i),0);
g.drawLine(dot5.x,dot5.y,dot6.x,dot6.y);
}
g.setColor(new Color(128,128,128));
for(int i=2;i<10;i++){
dot1=transformation(-120,-120,(30*(i+3)-150));
dot2=transformation(-130,-120,(30*(i+3)-150));
dot3=transformation(-120,-119,(30*(i+3)-150));
dot4=transformation(-120,120,(30*(i+3)-150));
g.drawLine(dot1.x,dot1.y,dot2.x,dot2.y);
g.drawLine(dot3.x,dot3.y,dot4.x,dot4.y);
g2.setFont(new Font ("SanSerif",Font.PLAIN,12));
g.drawString(rulerZ[(i+3)],dot2.x-38,dot2.y+5);
if(i==5) g.drawString("L",dot2.x-25,dot2.y-110);
}
// Coloring
for(int i=0;i<=EndingX;i++){
SmallestInnerPart[i]=EndingY;
LargestInnerPart[i]=0;
}
dot=new Point();
for(double x=120;x>=-120;x-=0.2)
for(double y=-120;y<=120;y+=0.2){
double transX=x/60;
double transY=y/120+1;
double transZ=function(transX,transY);
double z=transZ*15.2;
dot=transformation(x,y,z);
if(dot.y<SmallestInnerPart[dot.x]){
SmallestInnerPart[dot.x]=dot.y;
g.setColor(gradation(z));
g.drawRect(dot.x,dot.y,1,1);
}
if(dot.y>LargestInnerPart[dot.x]){
LargestInnerPart[dot.x]=dot.y;
g.setColor(new Color(128,128,128));
g.drawRect(dot.x,dot.y,1,1);
}
}
}
public static double function(double x, double y){
double z;
double k0;
double k1;
double u;
u=Math.pow((2*Math.PI)*(y/ratio),(-0.5))*(Math.exp(-Math.pow((x-0.7),2)/(2*y/ratio))+Math.exp
(-Math.pow((x+0.7),2)/(2*y/ratio)))/2;
k0=Math.pow(exp,2)/var+2;
k1=Math.pow(exp,3)/var+exp;
z=Math.pow(y,(-k0-1))*Math.exp((-k1)/(y))*u;
if(y>=0){
if(z>=0){
if(u>=0)
return 80*z;
else return 0;
}
else return 0;
}
else return 0;
}
public Color gradation(double z){
int d,r,g,b;
z=z*5.2;
if(z>=0) d=(int)z % 256;
else d=255-(-(int)z % 256);
int c=(int)(d/85.334);
switch(c){
case 0: r=79+76*d/86;
g=129+58*d/86;
b=189-100*d/86;
break;
case 1: r=155+37*(d-86)/85;
g=187-99*(d-86)/85;
b=89-12*(d-86)/85;
break;
case 2: r=192-113*(d-171)/84;
g=88+41*(d-171)/84;
b=77+112*(d-171)/84;
break;
default: r=0; g=0; b=0;
break;
}
Color color=new Color(r,g,b);
return color;
}
public Point transformation(double x,double y,double z){
Point dot=new Point();
dot.x=StartingX+(int)((x+120)+Math.cos(Math.toRadians(30))*(y+120)/2);
dot.y=StartingY-(int)(Math.sin(Math.toRadians(30))*(y+120)/2+(z+120));
return dot;
}
}
3. The Estimation of The Posterior Distribution
The example of the conditional likelihood function is given below.![]()
![$$L\left( y_B|\theta \right) = \prod_{i=11}^{20}{\left[ \frac{1}{\sqrt{2\pi\sigma^2}} \exp{\left( -\frac{\left( y_i-\mu\right)^2}{2\sigma^2} \right)}\times \frac{1}{2}\right] }$$ $$L\left( y_B|\theta \right) = \prod_{i=11}^{20}{\left[ \frac{1}{\sqrt{2\pi\sigma^2}} \exp{\left( -\frac{\left( y_i-\mu\right)^2}{2\sigma^2} \right)}\times \frac{1}{2}\right] }$$](http://paulownia.sakura.ne.jp/materials/learning_journals/archives/eqn19.png)
The posterior distribution is in proportion to the
product of the conditional likelihood function
multiplied by the prior distribution and the
example with weight wj is given below.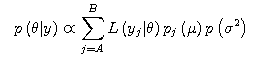
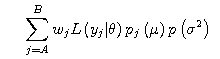
source code: PosteriorMultiModal.java
import java.awt.*;
import java.awt.event.*;
import java.applet.Applet;
import javax.swing.JLabel;
import javax.swing.JTextField;
public class PosteriorMultiModal extends Applet implements
ActionListener{
// variable set
private static final long serialVersionUID = -3578181170658236841L;
final static int StartingX=50,StartingY=527;
final static String[] rulerX = {"",""," -1.6",""," -0.8",""," 0",""," 0.8",""," 1.6",""};
final static String[] rulerY = {"",""," 0.2",""," 0.6",""," 1.0",""," 1.4",""," 1.8",""};
final static String[] rulerZ = {"","","","",""," 0","","","","","","","",""};
final int EndingX=StartingX+transformation(120,120,120).x;
final int EndingY=StartingY+transformation(120,-120,-120).y;
public int[] SmallestInnerPart=new int[EndingX+1];
public int[] LargestInnerPart=new int[EndingX+1];
public static double exp = 1.0;
public static double var = 1.0;
public static double ratio = 10.0;
JTextField yx = new JTextField("1.0");
JTextField yn = new JTextField("1.0");
JTextField yr = new JTextField("10.0");
JLabel label1 = new JLabel("The Posterior Distribution",JLabel.CENTER);
JLabel label2 = new JLabel("<html><body><font size=3>The Expectation of σ<sup>2</sup> (0<E(σ<sup>2</sup>)≤2.0)/font></body></html>", JLabel.CENTER);
JLabel label3 = new JLabel("<html><body><font size=3>The Variance of σ<sup>2</sup> (0<Var(σ<sup>2</sup>)≤10<sup>8</sup>)</font></body></html>", JLabel.CENTER);
JLabel label4 = new JLabel("<html><body><font size=3>The Ratio of σ<sup>2</sup> to Var(μ<sub>j</sub>) (0<r≤
10<sup>8</sup>)</font></body></html>", JLabel.CENTER);
public void init(){
label1.setPreferredSize(new Dimension(400,24));
label1.setFont(new Font("Serif",Font.BOLD,15));
add(label1);
label2.setPreferredSize(new Dimension(260,23));
label2.setFont(new Font("Serif",Font.BOLD,11));
add(label2);
yx.setPreferredSize(new Dimension(120,23));
add(yx);
label3.setPreferredSize(new Dimension(260,23));
label3.setFont(new Font("Serif",Font.BOLD,11));
add(label3);
yn.setPreferredSize(new Dimension(120,23));
add(yn);
label4.setPreferredSize(new Dimension(260,23));
label4.setFont(new Font("Serif",Font.BOLD,11));
add(label4);
yr.setPreferredSize(new Dimension(120,23));
add(yr);
yx.addActionListener(this);
yn.addActionListener(this);
yr.addActionListener(this);
}
public void actionPerformed(ActionEvent e){
if(e.getSource()==yx){exp = Double.valueOf(yx.getText()).doubleValue();
if(exp <= 0 || exp > 2.0){exp=1.0;
}
}
if(e.getSource()==yn){var = Double.valueOf(yn.getText()).doubleValue();
if(var <= 0 || var > Math.pow(10.0,8)){var=1.0;
}
}
if(e.getSource()==yr){ratio = Double.valueOf(yr.getText()).doubleValue();
if(ratio <= 0 || ratio > Math.pow(10.0,8))
{ratio=10.0;
}
}
yx.setText(""+exp);
yn.setText(""+var);
yr.setText(""+ratio);
repaint();
}
public void paint(Graphics g){
Point dot,dot1,dot2,dot3,dot4,dot5,dot6;
Graphics2D g2 = (Graphics2D)g;
GradientPaint gp1 = new GradientPaint(0, 0, new Color(154,181,228), 0,470,new Color(225,232,245), true);
g2.setPaint(gp1);
g2.fillRect(0,0,460,447);
super.paint(g);
// x axis
g.setColor(new Color(128,128,128));
dot1=transformation(-120,-120,0);
dot2=transformation(120,-120,0);
g.drawLine(dot1.x,dot1.y,dot2.x,dot2.y);
for(int i=0;i<21;i++){
dot1=transformation((120/10*i-120),-120,0);
if(i % 4==0){
dot2=transformation((120/10*i-120),(-120-10),0);
g.setColor(new Color(128,128,128));
g.drawLine(dot1.x,dot1.y,dot2.x,dot2.y);
g2.setFont(new Font ("SanSerif",Font.PLAIN,12));
g.drawString(rulerX[i/2],dot2.x-48,dot2.y+15);
if(i==8)
g.drawString("μ",dot2.x+28,dot2.y+30);
}
}
// y axis
g.setColor(new Color(128,128,128));
dot1=transformation(-120,-120,0);
dot2=transformation(-120,120,0);
dot3=transformation(-120,120,0);
dot4=transformation(-120,120,210);
dot5=transformation(120,-120,0);
dot6=transformation(120,120,0);
g.drawLine(dot1.x,dot1.y,dot2.x,dot2.y);
g.drawLine(dot3.x,dot3.y,dot4.x,dot4.y);
g.drawLine(dot5.x,dot5.y,dot6.x,dot6.y);
for(int i=0;i<210;i=i+1){
dot3=transformation(-119,120,i);
dot4=transformation(120,120,i);
g.setColor(new Color(154,181,228));
g.drawLine(dot3.x,dot3.y,dot4.x,dot4.y);
}
g.setColor(new Color(128,128,128));
for(int i=3;i<10;i++){
dot3=transformation(-120,120,(12/4*(i+3)-15)*10);
dot4=transformation(120,120,(12/4*(i+3)-15)*10);
g.drawLine(dot3.x,dot3.y,dot4.x,dot4.y);
}
for(int i=0;i<21;i++){
dot1=transformation(120,(12*i-120),0);
if(i % 4==0){
dot2=transformation((12+1)*10,(12*i-120),0);
g.setColor(new Color(128,128,128));
g.drawLine(dot1.x,dot1.y,dot2.x,dot2.y);
g.setFont(new Font ("SanSerif",Font.PLAIN,12));
g.drawString(rulerY[i/2],dot2.x-10,dot2.y+13);
if(i==8) g.drawString("σ",dot2.x+38,dot2.y+16);
g2.setFont(new Font ("SanSerif",Font.PLAIN,8));
if(i==8) g.drawString("2",dot2.x+47,dot2.y+9);
}
}
// z axis
g.setColor(new Color(128,128,128));
dot1=transformation(-120,-120,0);
dot2=transformation(-120,-120,210);
dot3=transformation(-120,119,210);
dot4=transformation(-120,119,0);
g.drawLine(dot1.x,dot1.y,dot2.x,dot2.y);
g.drawLine(dot2.x,dot2.y,dot3.x,dot3.y);
g.drawLine(dot3.x,dot3.y,dot4.x,dot4.y);
for(int i=0;i<240;i=i+1){
g.setColor(new Color(154,181,228));
dot5=transformation(-120,(-119+i),210);
dot6=transformation(-120,(-119+i),0);
g.drawLine(dot5.x,dot5.y,dot6.x,dot6.y);
}
g.setColor(new Color(128,128,128));
for(int i=2;i<10;i++){
dot1=transformation(-120,-120,(30*(i+3)-150));
dot2=transformation(-130,-120,(30*(i+3)-150));
dot3=transformation(-120,-119,(30*(i+3)-150));
dot4=transformation(-120,120,(30*(i+3)-150));
g.drawLine(dot1.x,dot1.y,dot2.x,dot2.y);
g.drawLine(dot3.x,dot3.y,dot4.x,dot4.y);
g2.setFont(new Font ("SanSerif",Font.PLAIN,12));
g.drawString(rulerZ[(i+3)],dot2.x-38,dot2.y+5);
if(i==5) g.drawString("L",dot2.x-25,dot2.y-110);
}
// Coloring
for(int i=0;i<=EndingX;i++){
SmallestInnerPart[i]=EndingY;
LargestInnerPart[i]=0;
}
dot=new Point();
for(double x=120;x>=-120;x-=0.2)
for(double y=-120;y<=120;y+=0.2){
double transX=x/60;
double transY=y/120+1;
double transZ=function(transX,transY);
double z=transZ*3.8;
dot=transformation(x,y,z);
if(dot.y<SmallestInnerPart[dot.x]){
SmallestInnerPart[dot.x]=dot.y;
g.setColor(gradation(z));
g.drawRect(dot.x,dot.y,1,1);
}
if(dot.y>LargestInnerPart[dot.x]){
LargestInnerPart[dot.x]=dot.y;
g.setColor(new Color(128,128,128));
g.drawRect(dot.x,dot.y,1,1);
}
}
}
public static double function(double x, double y){
double z1;
double z2;
double k0;
double k1;
double u1;
double u2;
double d01=1;
double d02=1;
double[] d1= new double[21];
double[] d2={-2.18,-1.19,-0.74,-1.2,-2.53,-0.5,0.09,0.31,-1.71,-0.67};
double[] d3= new double[21];
double[] d4= {0.59,0.13,1.22,0.45,-0.22,0.15,1.5,1.06,1.32,1.88};
for(int i=0;i<10;i++){
d1[i]=Math.pow(2*Math.PI*y,(-0.5))*Math.exp(-Math.pow((d2[i]-x),2)/(2*y));
d01=2.4*d01*d1[i];
}
for(int i=0;i<10;i++){
d3[i]=Math.pow(2*Math.PI*y,(-0.5))*Math.exp(-Math.pow((d4[i]-x),2)/(2*y));
d02=2.4*d02*d3[i];
}
u1=Math.pow((2*Math.PI)*(y/ratio),(-0.5))*Math.exp(-Math.pow((x+0.7),2)/(2*y/ratio));
u2=Math.pow((2*Math.PI)*(y/ratio),(-0.5))*Math.exp(-Math.pow((x-0.7),2)/(2*y/ratio));
k0=Math.pow(exp,2)/var+2;
k1=Math.pow(exp,3)/var+exp;
z1=9*Math.pow(y,(-k0-1))*Math.exp((-k1)/(y))*u1;
z2=9*Math.pow(y,(-k0-1))*Math.exp((-k1)/(y))*u2;
if(y>=0){
if(z1>=0 && z2>=0){
if(u1>=0 && u2>=0)
return 1200*d01*z1+36*d02*z2;
else return 0;
}
else return 0;
}
else return 0;
}
public Color gradation(double z){
int d,r,g,b;
z=z*5.2;
if(z>=0) d=(int)z % 256;
else d=255-(-(int)z % 256);
int c=(int)(d/85.334);
switch(c){
case 0: r=79+76*d/86;
g=129+58*d/86;
b=189-100*d/86;
break;
case 1: r=155+37*(d-86)/85;
g=187-99*(d-86)/85;
b=89-12*(d-86)/85;
break;
case 2: r=192-113*(d-171)/84;
g=88+41*(d-171)/84;
b=77+112*(d-171)/84;
break;
default: r=0; g=0; b=0;
break;
}
Color color=new Color(r,g,b);
return color;
}
public Point transformation(double x,double y,double z){
Point dot=new Point();
dot.x=StartingX+(int)((x+120)+Math.cos(Math.toRadians(30))*(y+120)/2);
dot.y=StartingY-(int)(Math.sin(Math.toRadians(30))*(y+120)/2+(z+120));
return dot;
}
}
4. The Metropolis Sampler algorithm
The example of the Metropolis sampler is given
below.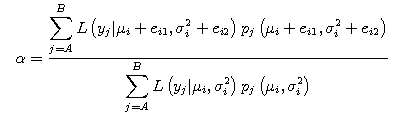
![]()
![]()
We accept μ*i+1 and σ*2i+1 when α meets the below conditions.![]()
![]()
![]()
We reject the above μ* i+1 and σ*2i+1 and accept the below μ*i+1 and σ*2i+1 when α meets the below condition.![]()
![]()
source code: Metropolis.java
import java.awt.*;
import java.awt.event.*;
import java.text.DecimalFormat;
import java.applet.Applet;
import javax.swing.JLabel;
import javax.swing.JTextField;
public class Metropolis extends Applet implements ActionListener{
// variable set
private static final long serialVersionUID = 8565245775496766530L;
public static double exp = 1.0;
public static double var = 1.0;
public static double ratio = 10.0;
public static double u, d3, d4, d7, d8, d9, d10, d11, d12;
public static double[] s1 = new double[10000];
public static double[] s2 = new double[10000];
public static double[] s3 = new double[1000];
public static double[] s4 = new double[1000];
public static double[] se1 = new double[10000];
public static double[] se2 = new double[10000];
public static double[] d1 = new double[10000];
public static double[] d2 = new double[10000];
public static double[] d5 = new double[10000];
public static double[] d6 = new double[10000];
JTextField yx = new JTextField("1.0");
JTextField yn = new JTextField("1.0");
JTextField yr = new JTextField("10.0");
JLabel label1 = new JLabel("The Metropolis Sampler Frequency Distribution",JLabel.CENTER);
JLabel label2 = new JLabel("<html><body><font size=3>The Expectation of σ<sup>2</sup> (0<E(σ<sup>2</sup>)≤10<sup>8</sup>)</font></body></html>",JLabel.CENTER);
JLabel label3 = new JLabel("<html><body><font size=3>The Variance of σ<sup>2</sup> (0<Var(σ<sup>2</sup>)≤10<sup>8</sup>)</font></body></html>",JLabel.CENTER);
JLabel label4 = new JLabel("<html><body><font size=3>The Ratio of σ<sup>2</sup> to Var(μ<sub>j</sub>) (0<r≤10<sup>8</sup>)</font></body></html>", JLabel.CENTER);
public void init(){
label1.setPreferredSize(new Dimension(416,24));
label1.setFont(new Font("Serif",Font.BOLD,14));
add(label1);
label2.setPreferredSize(new Dimension(260,23));
label2.setFont(new Font("Serif",Font.BOLD,11));
add(label2);
yx.setPreferredSize(new Dimension(80,23));
add(yx);
label3.setPreferredSize(new Dimension(260,23));
label3.setFont(new Font("Serif",Font.BOLD,11));
add(label3);
yn.setPreferredSize(new Dimension(80,23));
add(yn);
label4.setPreferredSize(new Dimension(260,23));
label4.setFont(new Font("Serif",Font.BOLD,11));
add(label4);
yr.setPreferredSize(new Dimension(80,23));
add(yr);
yx.addActionListener(this);
yn.addActionListener(this);
yr.addActionListener(this);
}
public void actionPerformed(ActionEvent e){
if(e.getSource()==yx){
exp=Double.valueOf(yx.getText()).doubleValue();
if(exp <= 0 || exp > Math.pow(10.0,8)){
exp = 1.0;
}
}
if(e.getSource()==yn){
var = Double.valueOf(yn.getText()).doubleValue();
if(var <= 0 || var > Math.pow(10.0,8)){
var = 1.0;
}
}
if(e.getSource()==yr){ratio = Double.valueOf(yr.getText()).doubleValue();
if(ratio <= 0 || ratio > Math.pow(10.0,8))
{ratio = 10.0;}
}
yx.setText(""+exp);
yn.setText(""+var);
yr.setText(""+ratio);
repaint();
}
public void paint(Graphics g){
double z1,z2,ss1,ss2;
s1[0] = 0.0;
s2[0] = 1.0;
z1=function(s1[0],s2[0]);
for(int i=0;i<9999;i++){
se1[i]=normal.sampleNormal(0,0.5);
se2[i]=normal.sampleNormal(0,0.002);
ss1=s1[i]+se1[i];
ss2=s2[i]+se2[i];
z2=function(ss1,ss2);
if(z2/z1>=1){
s1[i+1]=ss1;
s2[i+1]=ss2;
z1=z2;
}
else if(z2/z1>=normal.sampleNormal(0,1)){
s1[i+1]=ss1;
s2[i+1]=ss2;
z1=z2;
}
else {
s1[i+1]=s1[i];
s2[i+1]=s2[i];
}
}
d1[5000]=s1[5000];
d2[5000]=s2[5000];
for(int i=5001;i<10000;i++){
d1[i]=d1[i-1]+s1[i];
d2[i]=d2[i-1]+s2[i];
}
d3=d1[9999]/5000;
d4=d2[9999]/5000;
d5[4999]=0;
d6[4999]=0;
for(int i=5000;i<10000;i++){
d5[i]=Math.pow((s1[i]-d3),2)+d5[i-1];
d6[i]=Math.pow((s2[i]-d4),2)+d6[i-1];
}
d7=d5[9999]/(5000-1);
d8=d6[9999]/(5000-1);
// variable set
int[] xxxx = new int[1000];
int[] yyyy = new int[1000];
int[] xxxx1 = new int[1000];
int[] yyyy1 = new int[1000];
double minss1 = s1[5000];
double maxss1 = s1[5000];
double minss2 = s2[5000];
double maxss2 = s2[5000];
for(int i=5000;i<10000;i++){
if(s1[i]>maxss1){
maxss1 = s1[i];
}
}
for(int i=5000;i<10000;i++){
if(s1[i]<minss1){
minss1 = s1[i];
}
}
for(int i=5000;i<10000;i++){
if(s2[i]>maxss2){
maxss2 = s2[i];
}
}
for(int i=5000;i<10000;i++){
if(s2[i]<minss2){
minss2 = s2[i];
}
}
for(int i=0;i<1000;i++){
s3[i]=0;
s4[i]=0;
}
double aaa=(maxss1-minss1)/1000;
double bbb=(maxss2-minss2)/1000;
for(int i=5000;i<10000;i++){
for(int j=0;j<1000;j++){
if(s1[i] >= (minss1+aaa*j) && s1[i] < minss1+aaa*(j+1))
s3[j]=(s3[j]+1.0);
}
}
for(int i=5000;i<10000;i++){
for(int j=0;j<1000;j++){
if(minss2+bbb*j<=s2[i] && s2[i] < minss2+bbb*(j+1))
s4[j]=s4[j]+1;
}
}
// variable set
double minss3 = s3[0];
double maxss3 = s3[0];
double minss4 = s4[0];
double maxss4 = s4[0];
for(int i=0;i<1000;i++){
if(maxss3<s3[i]){
maxss3 = s3[i];
}
}
for(int i=0;i<1000;i++){
if(s3[i]<minss3){
minss3 = s3[i];
}
}
for(int i=0;i<1000;i++){
if(s4[i]>maxss4){
maxss4 = s4[i];
}
}
for(int i=0;i<1000;i++){
if(s4[i]<minss4){
minss4 = s4[i];
}
}
double yyy = maxss3-minss3;
double yyy1 = maxss4-minss4;
for(int i=0;i<1000;i++){
xxxx[i] = (int)(i*351/1000)+33;
yyyy[i] = 474-(int)((s3[i]-minss3)*351/yyy);
xxxx1[i] = (int)(i*351/1000)+33;
yyyy1[i] = 474-(int)((s4[i]-minss4)*351/yyy1);
}
Graphics2D g2 = (Graphics2D)g;
GradientPaint gp1 = new GradientPaint(0, 0, new Color(154,181,228), 0,470,new Color(225,232,245), true);
g2.setPaint(gp1);
g2.fillRect(0,0,416,503);
super.paint(g);
GradientPaint gp2 = new GradientPaint(0, 33, new Color(225,232,245), 0,351,new Color(154,181,228),true);
g2.setPaint(gp2);
g2.fillRect(33,123,354,351);
GradientPaint gp4 = new GradientPaint(33, 227, new Color(192,88,77), 33,418,new Color(160,82,45), true);
g2.setPaint(gp4);
for (int i=0;i<1000;i++){
g2.drawLine(xxxx[i], 474, xxxx[i], yyyy[i]);
}
DecimalFormat df = new DecimalFormat("0.00");
g2.setFont(new Font ("Serif",Font.BOLD,12));
g2.setColor (new Color(0,0,0));
g2.drawString("n = 5000",280,157);
g2.setColor (new Color(0,0,0));
g2.setFont(new Font ("Serif",Font.BOLD,12));
g2.drawString("E(μ",280,177);
g2.setFont(new Font ("Serif",Font.BOLD,12));
g2.drawString("*",300,176);
g2.setFont(new Font ("Serif",Font.BOLD,12));
g2.drawString("|y) =",305,177);
g2.drawString(df.format(d3),335,177);
g2.drawString("Var(μ",280,197);
g2.setFont(new Font ("Serif",Font.BOLD,12));
g2.drawString("*",312,196);
g2.setFont(new Font ("Serif",Font.BOLD,12));
g2.drawString("|y) =",317,197);
g2.drawString(df.format(d7),347,197);
g2.setColor (new Color(0,0,0));
g2.drawString("E(σ",280,217);
g2.setFont(new Font ("Serif",Font.BOLD,12));
g2.drawString("*",300,216);
g2.setFont(new Font ("Serif",Font.BOLD,8));
g2.drawString("2",305,212);
g2.setFont(new Font ("Serif",Font.BOLD,12));
g2.drawString("|y) =",310,217);
g2.drawString(df.format(d4),340,217);
g2.drawString("Var(σ",280,237);
g2.setFont(new Font ("Serif",Font.BOLD,12));
g2.drawString("*",312,236);
g2.setFont(new Font ("Serif",Font.BOLD,8));
g2.drawString("2",317,232);
g2.setFont(new Font ("Serif",Font.BOLD,12));
g2.drawString("|y) =",322,237);
g2.drawString(df.format(d8),352,237);
g2.drawString("E(y) = -0.11",280,257);
g2.drawString("Var(y) = 1.52",280,277);
g2.setColor (new Color(0,0,0));
g2.drawString("F",15,143);
g2.setColor (new Color(79,129,189));
g2.setColor (new Color(192,88,77));
g2.drawString("μ",360,488);
}
public static double function(double x, double y){
double z1;
double z2;
double k0;
double k1;
double u1;
double u2;
double d01=1;
double d02=1;
double[] f1= new double[10];
double[] f2={-2.18,-1.19,-0.74,-1.2,-2.53,-0.5,0.09,0.31,-1.71,-0.67};
double[] f3= new double[10];
double[] f4={0.59,0.13,1.22,0.45,-0.22,0.15,1.5,1.06,1.32,1.88};
for(int i=0;i<10;i++){
f1[i]=Math.pow(2*Math.PI*y,(-0.5))*Math.exp(-Math.pow(f2[i]-x,2)/(2*y));
d01=d01*f1[i];
}
for(int i=0;i<10;i++){
f3[i]=Math.pow(2*Math.PI*y,(-0.5))*Math.exp(-Math.pow(f4[i]-x,2)/(2*y));
d02=d02*f3[i];
}
u1=Math.pow((2*Math.PI)*(y/ratio),(-0.5))*(Math.exp(-Math.pow((x+0.7),2)/(2*y/ratio)));
u2=Math.pow((2*Math.PI)*(y/ratio),(-0.5))*(Math.exp(-Math.pow((x-0.7),2)/(2*y/ratio)));
k0=Math.pow(exp,2)/var+2;
k1=Math.pow(exp,3)/var+exp;
z1=Math.pow(k1,k0)/GammaF.gamma(k0)*Math.pow(y,(-k0-1))*Math.exp((-k1)/(y))*u1;
z2=Math.pow(k1,k0)/GammaF.gamma(k0)*Math.pow(y,(-k0-1))*Math.exp((-k1)/(y))*u2;
if(y>=0){
if(z1>=0 && z2>=0){
if(u1>=0 && u2>=0)
return (d01*z1+d02*z2)/2;
else return 0;
}
else return 0;
}
else return 0;
}
}
source code: normal.java
import java.util.*;
public class normal {
private static Random rnd = new Random(Calendar.getInstance().
getTimeInMillis()+Thread.currentThread().getId());
private static double u;
public static double sampleNormal(double e0, double e1) {
double e2;
e2=Math.pow(e1,(0.5));
u=e2*rnd.nextGaussian()+e0;
return u;
}
}
GammaF.java
// See the below website, copy and paste the class "Gamma".
// Then modify the code as necessary.
//
// http://www.cs.princeton.edu/introcs/91float/Gamma.java.html
//
// I express my appreciation for Robert Sedgewick
// and Kevin Wayne.
In conclusion, the posterior distribution is bimodal because the conditional likelihood function is set to the bimodal form and the prior distribution is bimodal. The variances of μ and σ2 on the posterior distribution is smaller than the variances of μ and σ2 on the prior distribution because the posterior distribution is in proportion to the product of the conditional likelihood function and depends on the scatteration of the data.
Finally I am happy to assist you in coding and simulating a random process with the MCMC algorithm in JAVA.
・ This article uses three heavy java applets. So the images or the applets on your browser may act up under certaincircumstance.
・ How to deal with the problem is in waiting 30-60 seconds and not touching the keyboard and the mouse to display the correct images or applets on the browser.
This article is theoretically indebted to the scrupulous works of Yoshiyuki Wakui, Hiroshi Watanabe, and Takeshi Amemiya, which have a lot of lucid explanations and I'd very much appreciate their useful descriptions. In addition, I'd like to express my gratitude for some
helpful websites, such as http://codezine.jp/article/detail/116 as for how to make three-dimensional graph in JAVA and so on.
First I'd tentatively like to outline the situation we were put in with your agreement. A busy person generated normal random numbers with a computer. Then his phone rang. After he had answered the phone, someone
called out to him. After he had reluctantly wrapped up something urgent, he realized that he clean forgot the variance of the normal random variables. He barely remembered the mean and the form of the distribution. Unfortunately, he needed to generate the additional
normal random numbers which followed the almost same normal distribution.
1. The Data Set
The data set he generated is given below.
| n | 1 | 2 | 3 | 4 | 5 |
| y | 0.58 | -2.23 | 0.86 | 0.16 | -0.20 |
| n | 6 | 7 | 8 | 9 | 10 |
| y | 0.54 | 1.52 | -0.69 | 0.66 | -1.75 |
| n | 11 | 12 | 13 | 14 | 15 |
| y | -1.24 | 0.32 | -0.58 | -0.83 | -0.74 |
| n | 16 | 17 | 18 | 19 | 20 |
| y | -2.01 | -0.71 | -0.05 | 0.47 | 2.30 |
The sample mean is about -0.18 and the unbiased sample variance is about 1.33. These random variables y are actually generated from the normal distribution N(0,1) and he knew the population mean of y was 0 but didn't know the population variance of σ2 was 1. That is to say we pretend we don't know the population variance of σ2 is 1 and keep carrying out the below experiment on the above condition.
2. The Estimation of The Prior Distribution
I supposed that the mean μ of the random variables followed the normal distribution, that the population mean of μ is 0, that the population variance of μ is in proportion to the population variance of the random
variables, and that the variance σ2 of the random variables followed the inverse gamma distribution. The example of the prior distribution is given below.![]()
We substitute both p(μ) and p(σ2) in the above equation to find the prior distribution.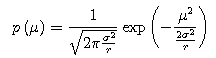
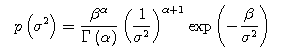
We also substitute the parameters for both E(σ2) and Var(σ2) in the below equations to find the value of both α and β.![]()
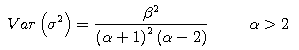
source code: PriorDistribution.java
import java.awt.*;
import java.awt.event.*;
import java.applet.Applet;
import javax.swing.JLabel;
import javax.swing.JTextField;
public class PriorDistribution extends Applet implements ActionListener{
// variable set
private static final long serialVersionUID = 4049271078937921933L;
final static int StartingX=50,StartingY=527;
final static String[] rulerX = {"",""," 0.2",""," 0.6",""," 1.0",""," 1.4",""," 1.8",""};
final static String[] rulerY = {"",""," -1.0",""," -0.5",""," 0",""," 0.5",""," 1.0",""};
final static String[] rulerZ = {"","","","",""," 0","","","","","","","",""};
final int EndingX=StartingX+transformation(120,120,120).x;
final int EndingY=StartingY+transformation(120,-120,-120).y;
public int[] SmallestInnerPart=new int[EndingX+1];
public int[] LargestInnerPart=new int[EndingX+1];
public static double exp = 1.0;
public static double var = 1.0;
public static double ratio = 3.0;
JTextField yx = new JTextField("1.0");
JTextField yn = new JTextField("1.0");
JTextField yr = new JTextField("3.0");
JLabel label1 = new JLabel("The Prior Distribution", JLabel.CENTER);
JLabel label2 = new JLabel("<html><body><font size=3>The Expectation of σ<sup>2</sup>(0<E(σ<sup>2</sup>)≤2.0)</font></body></html>", JLabel.CENTER);
JLabel label3 = new JLabel("<html><body><font size=3>The Variance of σ<sup>2</sup> (0<Var(σ<sup>2</sup>)≤10<sup>8</sup>)</font></body></html>", JLabel.CENTER);
JLabel label4 = new JLabel("<html><body><font size=3> The Ratio of σ<sup>2</sup> to Var(μ) (0<r≤10<sup>8</sup>)</font></body></html>",JLabel.CENTER);
public void init(){
label1.setPreferredSize(new Dimension(400,24));
label1.setFont(new Font("Serif",Font.BOLD,15));
add(label1);
label2.setPreferredSize(new Dimension(260,23));
label2.setFont(new Font("Serif",Font.BOLD,11));
add(label2);
yx.setPreferredSize(new Dimension(120,23));
add(yx);
label3.setPreferredSize(new Dimension(260,23));
label3.setFont(new Font("Serif",Font.BOLD,11));
add(label3);
yn.setPreferredSize(new Dimension(120,23));
add(yn);
label4.setPreferredSize(new Dimension(260,23));
label4.setFont(new Font("Serif",Font.BOLD,11));
add(label4);
yr.setPreferredSize(new Dimension(120,23));
add(yr);
yx.addActionListener(this);
yn.addActionListener(this);
yr.addActionListener(this);
}
public void actionPerformed(ActionEvent e){
if(e.getSource()==yx){
exp = Double.valueOf(yx.getText()).doubleValue();
if(exp <= 0 || exp > 2.0){exp=1.0;
}
}
if(e.getSource()==yn){
var = Double.valueOf(yn.getText()).doubleValue();
if(var <= 0 || var > Math.pow(10.0,8)){var=1.0;
}
}
if(e.getSource()==yr){
ratio = Double.valueOf(yr.getText()).doubleValue();
if(ratio <= 0 || ratio > Math.pow(10.0,8)){ratio=3.0;
}
}
yx.setText(""+exp);
yn.setText(""+var);
yr.setText(""+ratio);
repaint();
}
public void paint(Graphics g){
Point dot,dot1,dot2,dot3,dot4,dot5,dot6;
Graphics2D g2 = (Graphics2D)g;
GradientPaint gp1 = new GradientPaint(0, 0, new Color(154,181,228), 0,470,new Color(225,232,245), true);
g2.setPaint(gp1);
g2.fillRect(0,0,460,447);
super.paint(g);
// x axis
g.setColor(new Color(128,128,128));
dot1=transformation(-120,-120,0);
dot2=transformation(120,-120,0);
g.drawLine(dot1.x,dot1.y,dot2.x,dot2.y);
for(int i=0;i<21;i++){
dot1=transformation((120/10*i-120),-120,0);
if(i % 4==0){
dot2=transformation((120/10*i-120),(120-10),0);
g.setColor(new Color(128,128,128));
g.drawLine(dot1.x,dot1.y,dot2.x,dot2.y);
g2.setFont(new Font ("SanSerif",Font.PLAIN,12));
g.drawString(rulerX[i/2],dot2.x-48,dot2.y+15);
if(i==8)
g.drawString("σ",dot2.x+28,dot2.y+30);
g2.setFont(new Font ("SanSerif",Font.PLAIN,8));
if(i==8) g.drawString("2",dot2.x+37,dot2.y+23);
}
}
// y axis
g.setColor(new Color(128,128,128));
dot1=transformation(-120,-120,0);
dot2=transformation(-120,120,0);
dot3=transformation(-120,120,0);
dot4=transformation(-120,120,210);
dot5=transformation(120,-120,0);
dot6=transformation(120,120,0);
g.drawLine(dot1.x,dot1.y,dot2.x,dot2.y);
g.drawLine(dot3.x,dot3.y,dot4.x,dot4.y);
g.drawLine(dot5.x,dot5.y,dot6.x,dot6.y);
for(int i=0;i<210;i=i+1){
dot3=transformation(-119,120,i);
dot4=transformation(120,120,i);
g.setColor(new Color(154,181,228));
g.drawLine(dot3.x,dot3.y,dot4.x,dot4.y);
}
g.setColor(new Color(128,128,128));
for(int i=3;i<10;i++){
dot3=transformation(-120,120,(12/4*(i+3)-15)*10);
dot4=transformation(120,120,(12/4*(i+3)-15)*10);
g.drawLine(dot3.x,dot3.y,dot4.x,dot4.y);
}
for(int i=0;i<21;i++){
dot1=transformation(120,(12*i-120),0);
if(i % 4==0){
dot2=transformation((12+1)*10,(12*i-120),0);
g.setColor(new Color(128,128,128));
g.drawLine(dot1.x,dot1.y,dot2.x,dot2.y);
g.setFont(new Font ("SanSerif",Font.PLAIN,12));
g.drawString(rulerY[i/2],dot2.x-10,dot2.y+13);
if(i==8) g.drawString("μ",dot2.x+38,dot2.y+16);
}
}
// z axis
g.setColor(new Color(128,128,128));
dot1=transformation(-120,-120,0);
dot2=transformation(-120,-120,210);
dot3=transformation(-120,119,210);
dot4=transformation(-120,119,0);
g.drawLine(dot1.x,dot1.y,dot2.x,dot2.y);
g.drawLine(dot2.x,dot2.y,dot3.x,dot3.y);
g.drawLine(dot3.x,dot3.y,dot4.x,dot4.y);
for(int i=0;i<240;i=i+1){
g.setColor(new Color(154,181,228));
dot5=transformation(-120,(-119+i),210);
dot6=transformation(-120,(-119+i),0);
g.drawLine(dot5.x,dot5.y,dot6.x,dot6.y);
}
g.setColor(new Color(128,128,128));
for(int i=2;i<10;i++){
dot1=transformation(-120,-120,(30*(i+3)-150));
dot2=transformation(-130,-120,(30*(i+3)-150));
dot3=transformation(-120,-119,(30*(i+3)-150));
dot4=transformation(-120,120,(30*(i+3)-150));
g.drawLine(dot1.x,dot1.y,dot2.x,dot2.y);
g.drawLine(dot3.x,dot3.y,dot4.x,dot4.y);
g2.setFont(new Font ("SanSerif",Font.PLAIN,12));
g.drawString(rulerZ[(i+3)],dot2.x-38,dot2.y+5);
if(i==5) g.drawString("L",dot2.x-25,dot2.y-110);
}
// Coloring
for(int i=0;i<=EndingX;i++){
SmallestInnerPart[i]=EndingY;
LargestInnerPart[i]=0;
}
dot=new Point();
for(double x=120;x>=-120;x-=0.2)
for(double y=-120;y<=120;y+=0.2){
double transX=x/120+1;
double transY=y/120;
double transZ=function(transX,transY);
double z=transZ*3.8;
dot=transformation(x,y,z);
if(dot.y<SmallestInnerPart[dot.x]){
SmallestInnerPart[dot.x]=dot.y;
g.setColor(gradation(z));
g.drawRect(dot.x,dot.y,1,1);
}
if(dot.y>LargestInnerPart[dot.x]){
LargestInnerPart[dot.x]=dot.y;
g.setColor(new Color(128,128,128));
g.drawRect(dot.x,dot.y,1,1);
}
}
}
public static double function(double x, double y){
double z;
double k0;
double k1;
double u;
u=(Math.pow((2*Math.PI)*(x/ratio),(-0.5)))*Math.exp(-Math.pow((y-0),2)/(2*x/ratio));
k0=Math.pow(exp,2)/var+2;
k1=Math.pow(exp,3)/var+exp;
z=Math.pow(x,(-k0-1))*Math.exp((-k1)/(x))*u;
if(x>=0){
if(z>=0){
if(u>=0)
return 150*z;
else return 0;
}
else return 0;
}
else return 0;
}
public Color gradation(double z){
int d,r,g,b;
z=z*5.2;
if(z>=0) d=(int)z % 256;
else d=255-(-(int)z % 256);
int c=(int)(d/85.334);
switch(c){
case 0: r=79+76*d/86;
g=129+58*d/86;
b=189-100*d/86;
break;
case 1: r=155+37*(d-86)/85;
g=187-99*(d-86)/85;
b=89-12*(d-86)/85;
break;
case 2: r=192-113*(d-171)/84;
g=88+41*(d-171)/84;
b=77+112*(d-171)/84;
break;
default: r=0; g=0; b=0;
break;
}
Color color=new Color(r,g,b);
return color;
}
public Point transformation(double x,double y,double z){
Point dot=new Point();
dot.x=StartingX+(int)((x+120)+Math.cos(Math.toRadians(30))*(y+120)/2);
dot.y=StartingY-(int)(Math.sin(Math.toRadians(30))*(y+120)/2+(z+120));
return dot;
}
}
3. The Estimation of The Posterior Distribution
The example of the conditional likelihood function is
given below.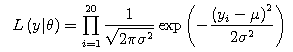
The posterior distribution is in proportion to the
product of the conditional likelihood function
multiplied by the prior distribution and its
example is given below.![]()
source code: PosteriorDistribution.java
import java.awt.*;
import java.awt.event.*;
import java.applet.Applet;
import javax.swing.JLabel;
import javax.swing.JTextField;
public class PosteriorDistribution extends Applet implements
ActionListener{
// variable set
private static final long serialVersionUID = -6251476488227240006L;
final static int StartingX=50,StartingY=527;
final static String[] rulerX = {"",""," 0.2",""," 0.6",""," 1.0",""," 1.4",""," 1.8",""};
final static String[] rulerY = {"",""," -1.0",""," -0.5",""," 0",""," 0.5",""," 1.0",""};
final static String[] rulerZ = {"","","","",""," 0","","","","","","","",""};
final int EndingX=StartingX+transformation(120,120,120).x;
final int EndingY=StartingY+transformation(120,-120,-120).y;
public int[] SmallestInnerPart=new int[EndingX+1];
public int[] LargestInnerPart=new int[EndingX+1];
public static double exp = 1.0;
public static double var = 1.0;
public static double ratio = 3.0;
JTextField yx = new JTextField("1.0");
JTextField yn = new JTextField("1.0");
JTextField yr = new JTextField("3.0");
JLabel label1 = new JLabel("The Posterior Distribution", JLabel.CENTER);
JLabel label2 = new JLabel("<html><body><font size=3>The Expectation of σ<sup>2</sup> (0<E(σ<sup>2</sup>)≤2.0)</font></body></html>", variJLabel.CENTER);
JLabel label3 = new JLabel("<html><body><font size=3>The Variance of σ<sup>2</sup> (0<Var(σ<sup>2</sup>)≤10<sup>8</sup>)</font></body></html>",JLabel.CENTER);
JLabel label4 = new JLabel("<html><body><font size=3>The Ratio of σ<sup>2</sup> to Var(μ) (0<r≤10<sup>8</sup>)</font></body></html>",JLabel.CENTER);
public void init(){
label1.setPreferredSize(new Dimension(400,24));
label1.setFont(new Font("Serif",Font.BOLD,15));
add(label1);
label2.setPreferredSize(new Dimension(260,23));
label2.setFont(new Font("Serif",Font.BOLD,11));
add(label2);
yx.setPreferredSize(new Dimension(120,23));
add(yx);
label3.setPreferredSize(new Dimension(260,23));
label3.setFont(new Font("Serif",Font.BOLD,11));
add(label3);
yn.setPreferredSize(new Dimension(120,23));
add(yn);
label4.setPreferredSize(new Dimension(260,23));
label4.setFont(new Font("Serif",Font.BOLD,11));
add(label4);
yr.setPreferredSize(new Dimension(120,23));
add(yr);
yx.addActionListener(this);
yn.addActionListener(this);
yr.addActionListener(this);
}
public void actionPerformed(ActionEvent e){
if(e.getSource()==yx){
exp = Double.valueOf(yx.getText()).doubleValue();
if(exp <= 0 || exp > 2.0){exp=1.0;
}
}
if(e.getSource()==yn){
var = Double.valueOf(yn.getText()).doubleValue();
if(var <= 0 || var > Math.pow(10.0,8)){
var=1.0;
}
}
if(e.getSource()==yr){
ratio = Double.valueOf(yr.getText()).doubleValue();
if(ratio <= 0 || ratio >Math.pow(10.0,8)){ratio=3.0;
}
}
yx.setText(""+exp);
yn.setText(""+var);
yr.setText(""+ratio);
repaint();
}
public void paint(Graphics g){
Point dot,dot1,dot2,dot3,dot4,dot5,dot6;
Graphics2D g2 = (Graphics2D)g;
GradientPaint gp1 = new GradientPaint(0, 0, new Color(154,181,228), 0,470,new Color(225,232,245), true);
g2.setPaint(gp1);
g2.fillRect(0,0,460,447);
super.paint(g);
// x axis
g.setColor(new Color(128,128,128));
dot1=transformation(-120,-120,0);
dot2=transformation(120,-120,0);
g.drawLine(dot1.x,dot1.y,dot2.x,dot2.y);
for(int i=0;i<21;i++){
dot1=transformation((120/10*i-120),-120,0);
if(i % 4==0){
dot2=transformation((120/10*i-120),(-120-10),0);
g.setColor(new Color(128,128,128));
g.drawLine(dot1.x,dot1.y,dot2.x,dot2.y);
g2.setFont(new Font ("SanSerif",Font.PLAIN,12));
g.drawString(rulerX[i/2],dot2.x-48,dot2.y+15);
if(i==8)
g.drawString("σ",dot2.x+28,dot2.y+30);
g2.setFont(new Font("SanSerif",Font.PLAIN,8));
if(i==8) g.drawString("2",dot2.x+37,dot2.y+23);
}
}
// y axis
g.setColor(new Color(128,128,128));
dot1=transformation(-120,-120,0);
dot2=transformation(-120,120,0);
dot3=transformation(-120,120,0);
dot4=transformation(-120,120,210);
dot5=transformation(120,-120,0);
dot6=transformation(120,120,0);
g.drawLine(dot1.x,dot1.y,dot2.x,dot2.y);
g.drawLine(dot3.x,dot3.y,dot4.x,dot4.y);
g.drawLine(dot5.x,dot5.y,dot6.x,dot6.y);
for(int i=0;i<210;i=i+1){
dot3=transformation(-119,120,i);
dot4=transformation(120,120,i);
g.setColor(new Color(154,181,228));
g.drawLine(dot3.x,dot3.y,dot4.x,dot4.y);
}
g.setColor(new Color(128,128,128));
for(int i=3;i<10;i++){
dot3=transformation(-120,120,(12/4*(i+3)-15)*10);
dot4=transformation(120,120,(12/4*(i+3)-15)*10);
g.drawLine(dot3.x,dot3.y,dot4.x,dot4.y);
}
for(int i=0;i<21;i++){
dot1=transformation(120,(12*i-120),0);
if(i % 4==0){
dot2=transformation((12+1)*10,(12*i-120),0);
g.setColor(new Color(128,128,128));
g.drawLine(dot1.x,dot1.y,dot2.x,dot2.y);
g.setFont(new Font ("SanSerif",Font.PLAIN,12));
g.drawString(rulerY[i/2],dot2.x-10,dot2.y+13);
if(i==8) g.drawString("μ",dot2.x+38,dot2.y+16);
}
}
// z axis
g.setColor(new Color(128,128,128));
dot1=transformation(-120,-120,0);
dot2=transformation(-120,-120,210);
dot3=transformation(-120,119,210);
dot4=transformation(-120,119,0);
g.drawLine(dot1.x,dot1.y,dot2.x,dot2.y);
g.drawLine(dot2.x,dot2.y,dot3.x,dot3.y);
g.drawLine(dot3.x,dot3.y,dot4.x,dot4.y);
for(int i=0;i<240;i=i+1){
g.setColor(new Color(154,181,228));
dot5=transformation(-120,(-119+i),210);
dot6=transformation(-120,(-119+i),0);
g.drawLine(dot5.x,dot5.y,dot6.x,dot6.y);
}
g.setColor(new Color(128,128,128));
for(int i=2;i<10;i++){
dot1=transformation(-120,-120,(30*(i+3)-150));
dot2=transformation(-130,-120,(30*(i+3)-150));
dot3=transformation(-120,-119,(30*(i+3)-150));
dot4=transformation(-120,120,(30*(i+3)-150));
g.drawLine(dot1.x,dot1.y,dot2.x,dot2.y);
g.drawLine(dot3.x,dot3.y,dot4.x,dot4.y);
g2.setFont(new Font ("SanSerif",Font.PLAIN,12));
g.drawString(rulerZ[(i+3)],dot2.x-38,dot2.y+5);
if(i==5) g.drawString("L",dot2.x-25,dot2.y-110);
}
// Coloring
for(int i=0;i<=EndingX;i++){
SmallestInnerPart[i]=EndingY;
LargestInnerPart[i]=0;
}
dot=new Point();
for(double x=120;x>=-120;x-=0.2)
for(double y=-120;y<=120;y+=0.2){
double transX=x/120+1;
double transY=y/120;
double transZ=function(transX,transY);
double z=transZ*3.8;
dot=transformation(x,y,z);
if(dot.y<SmallestInnerPart[dot.x]){
SmallestInnerPart[dot.x]=dot.y;
g.setColor(gradation(z));
g.drawRect(dot.x,dot.y,1,1);
}
if(dot.y>LargestInnerPart[dot.x]){
LargestInnerPart[dot.x]=dot.y;
g.setColor(new Color(128,128,128));
g.drawRect(dot.x,dot.y,1,1);
}
}
}
public static double function(double x, double y){
double z;
double k0;
double k1;
double u;
double d0=1;
double[] d1= new double[21];
double[] d2={0.58,-2.23,0.86,0.16,-0.20,0.54,1.52,-0.69,0.66,-1.75,-1.24,0.32,-0.58,-0.83,-0.74,-2.01,-0.71,-0.05,0.47,2.30};
for(int i=0;i<20;i++){
d1[i]=Math.pow(2*Math.PI*x,(-0.5))*Math.exp(-Math.pow((d2[i]-y),2)/(2*x));
d0=d0*d1[i];
}
u=(Math.pow((2*Math.PI)*(x/ratio),(-0.5)))*Math.exp(-Math.pow((y-0),2)/(2*x/ratio));
k0=Math.pow(exp,2)/var+2;
k1=Math.pow(exp,3)/var+exp;
z=160000000*Math.pow(x,(-k0-1))*Math.exp((-k1)/(x))*u;
if(x>=0){
if(z>=0){
if(u>=0)
return 100000000*d0*z;
else return 0;
}
else return 0;
}
else return 0;
}
public Color gradation(double z){
int d,r,g,b;
z=z*5.2;
if(z>=0) d=(int)z % 256;
else d=255-(-(int)z % 256);
int c=(int)(d/85.334);
switch(c){
case 0: r=79+76*d/86;
g=129+58*d/86;
b=189-100*d/86;
break;
case 1: r=155+37*(d-86)/85;
g=187-99*(d-86)/85;
b=89-12*(d-86)/85;
break;
case 2: r=192-113*(d-171)/84;
g=88+41*(d-171)/84;
b=77+112*(d-171)/84;
break;
default: r=0; g=0; b=0;
break;
}
Color color=new Color(r,g,b);
return color;
}
public Point transformation(double x,double y,double z){
Point dot=new Point();
dot.x=StartingX+(int)((x+120)+Math.cos(Math.toRadians(30))*(y+120)/2);
dot.y=StartingY-(int)(Math.sin(Math.toRadians(30))*(y+120)/2+(z+120));
return dot;
}
}
4. The Gibbs Sampler Algorithm
I am most grateful to the helpful website, MY STRUGGLE, and the URL is given below.
http://vyshemirsky.blogspot.com/2007/11/sample-from-gamma-distribution-in-java.html
The example of the Gibbs sampler is given below.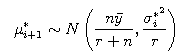
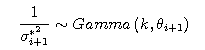
We substitute the shape parameter k and the scale parameter θi+1 in the probability density function of
the inverse gamma distribution and I provisionally set σ1*2 to 1.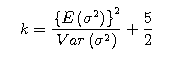
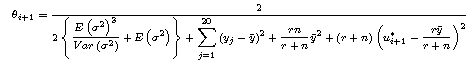
source code: GibbsSampler.java
import java.awt.*;
import java.awt.event.*;
import java.text.DecimalFormat;
import java.applet.Applet;
import javax.swing.JLabel;
import javax.swing.JTextField;
public class GibbsSampler extends Applet implements ActionListener{
// variable set
private static final long serialVersionUID = -729195055739028464L;
public static double exp = 1.0;
public static double var = 1.0;
public static double m0 = 3.0;
public static double u, d3, d4, d7, d8, d9, d10, d11, d12;
public static double[] s1 = new double[10000];
public static double[] s2 = new double[10000];
public static double[] s3 = new double[1000];
public static double[] s4 = new double[1000];
public static double[] d1 = new double[10000];
public static double[] d2 = new double[10000];
public static double[] d5 = new double[10000];
public static double[] d6 = new double[10000];
JTextField yx = new JTextField("1.0");
JTextField yn = new JTextField("1.0");
JTextField yr = new JTextField("3.0");
JLabel label1 = new JLabel("Gibbs Sampler Frequency Distribution",JLabel.CENTER);
JLabel label2 = new JLabel("<html><body><font size=3>The Expectation of σ<sup>2</sup> (0<E(σ<sup>2</sup>)≤10<sup>8</sup>)</font></body></html>",JLabel.CENTER);
JLabel label3 = new JLabel("<html><body><font size=3>The Variance of σ<sup>2</sup> (0<Var(σ<sup>2</sup>)≤10<sup>8</sup>)</font></body></html>",JLabel.CENTER);
JLabel label4 = new JLabel("<html><body><font size=3>The Ratio of σ<sup>2</sup> to Var(μ) (0<r≤10<sup>8</sup>)</font></body></html>",JLabel.CENTER);
public void init(){
label1.setPreferredSize(new Dimension(416,24));
label1.setFont(new Font("Serif",Font.BOLD,14));
add(label1);
label2.setPreferredSize(new Dimension(260,23));
label2.setFont(new Font("Serif",Font.BOLD,11));
add(label2);
yx.setPreferredSize(new Dimension(80,23));
add(yx);
label3.setPreferredSize(new Dimension(260,23));
label3.setFont(new Font("Serif",Font.BOLD,11));
add(label3);
yn.setPreferredSize(new Dimension(80,23));
add(yn);
label4.setPreferredSize(new Dimension(260,23));
label4.setFont(new Font("Serif",Font.BOLD,11));
add(label4);
yr.setPreferredSize(new Dimension(80,23));
add(yr);
yx.addActionListener(this);
yn.addActionListener(this);
yr.addActionListener(this);
}
public void actionPerformed(ActionEvent e){
if(e.getSource()==yx){
exp=Double.valueOf(yx.getText()).doubleValue();
if(exp <= 0 || exp > Math.pow(10.0,8)){
exp = 1.0;
}
}
if(e.getSource()==yn){
var = Double.valueOf(yn.getText()).doubleValue();
if(var <= 0 || var > Math.pow(10.0,8)){
var = 1.0;
}
}
if(e.getSource()==yr){m0 = Double.valueOf(yr.getText()).doubleValue();
if(m0 <= 0 || m0 > Math.pow(10.0,8))
{m0 = 3.0;}
}
yx.setText(""+exp);
yn.setText(""+var);
yr.setText(""+m0);
repaint();
}
public void paint(Graphics g){
double n = 20;
double n0 = 2*Math.pow(exp,2)/var+4;
double s0 = 2*(Math.pow(exp,3)/var+exp)/n0;
double u0 = 0;
double q = 25.31;
double ExpX = -0.18;
double m1 = m0+n;
double n1 = n0+n;
double n1s1 = n0*s0+q+(m0*n/(m0+n))*(ExpX-u0)*(ExpX-u0);
double u1 = (n*ExpX+m0*u0)/(m0+n);
s1[0]=1;
s2[0]=normal.sampleNormal(u1,(1/s1[0])/m1);
for(int i=0;i<9999;i++){
s1[i+1]=gamma.sampleGamma((n1+1)/2,1/(n1s1/2+m1*Math.pow(s2[i]-u1,2)/2));
s2[i+1]=normal.sampleNormal(u1,(1/s1[i+1])/m1);
}
d1[5000]=1/s1[5000];
d2[5000]=s2[5000];
for(int i=5001;i<10000;i++){
d1[i]=d1[i-1]+1/s1[i];
d2[i]=d2[i-1]+s2[i];
}
d3=d1[9999]/5000;
d4=d2[9999]/5000;
d5[4999]=0;
d6[4999]=0;
for(int i=5000;i<10000;i++){
d5[i]=Math.pow((1/s1[i]-d3),2)+d5[i-1];
d6[i]=Math.pow((s2[i]-d4),2)+d6[i-1];
}
d7=d5[9999]/(5000-1);
d8=d6[9999]/(5000-1);
// variable set
int[] xxxx = new int[1000];
int[] yyyy = new int[1000];
int[] xxxx1 = new int[1000];
int[] yyyy1 = new int[1000];
double minss1 = 1/s1[5000];
double maxss1 = 1/s1[5000];
double minss2 = s2[5000];
double maxss2 = s2[5000];
for(int i=5000;i<10000;i++){
if(1/s1[i]>maxss1){
maxss1 = 1/s1[i];
}
}
for(int i=5000;i<10000;i++){
if(1/s1[i]<minss1){
minss1 = 1/s1[i];
}
}
for(int i=5000;i<10000;i++){
if(s2[i]>maxss2){
maxss2 = s2[i];
}
}
for(int i=5000;i<10000;i++){
if(s2[i]<minss2){
minss2 = s2[i];
}
}
for(int i=0;i<1000;i++){
s3[i]=0;
s4[i]=0;
}
double aaa=(maxss1-minss1)/1000;
double bbb=(maxss2-minss2)/1000;
for(int i=5000;i<10000;i++){
for(int j=0;j<1000;j++){
if(1/s1[i] >= (minss1+aaa*j) && 1/s1[i] < minss1+aaa*(j+1))
s3[j]=(s3[j]+1.0);
}
}
for(int i=5000;i<10000;i++){
for(int j=0;j<1000;j++){
if(minss2+bbb*j<=s2[i] && s2[i]<minss2+bbb*(j+1))
s4[j]=s4[j]+1;
}
}
// variable set
double minss3 = s3[0];
double maxss3 = s3[0];
double minss4 = s4[0];
double maxss4 = s4[0];
for(int i=0;i<1000;i++){
if(maxss3<s3[i]){
maxss3 = s3[i];
}
}
for(int i=0;i<1000;i++){
if(s3[i]<minss3){
minss3 = s3[i];
}
}
for(int i=0;i<1000;i++){
if(s4[i]>maxss4){
maxss4 = s4[i];
}
}
for(int i=0;i<1000;i++){
if(s4[i]<minss4){
minss4 = s4[i];
}
}
double yyy = maxss3-minss3;
double yyy1 = maxss4-minss4;
for(int i=0;i<1000;i++){
xxxx[i] = (int)(i*351/1000)+33;
yyyy[i] = 474-(int)((s3[i]-minss3)*351/yyy);
xxxx1[i] = (int)(i*351/1000)+33;
yyyy1[i] = 474-(int)((s4[i]-minss4)*351/yyy1);
}
Graphics2D g2 = (Graphics2D)g;
GradientPaint gp1 = new GradientPaint(0, 0, new Color(154,181,228), 0,470,new Color(225,232,245), true);
g2.setPaint(gp1);
g2.fillRect(0,0,416,503);
super.paint(g);
GradientPaint gp2 = new GradientPaint(0, 33, new Color(225,232,245), 0,351,new Color(154,181,228), true);
g2.setPaint(gp2);
g2.fillRect(33,123,354,351);
GradientPaint gp3 = new GradientPaint(33, 227, new Color(79,129,189), 33,418,new Color(65,105,225), true);
g2.setPaint(gp3);
for (int i=0;i<1000;i++){
g2.drawLine(xxxx1[i], 474, xxxx1[i], yyyy1[i]);
}
GradientPaint(33, 227, new Color(192,88,77), 33,418,new Color(160,82,45), true);
g2.setPaint(gp4);
for (int i=0;i<1000;i++){
g2.drawLine(xxxx[i], 474, xxxx[i], yyyy[i]);
}
DecimalFormat df = new DecimalFormat("0.00");
g2.setFont(new Font ("Serif",Font.BOLD,12));
g2.setColor (new Color(0,0,0));
g2.drawString("n = 5000",280,157);
g2.setColor (new Color(0,0,0));
g2.setFont(new Font ("Serif",Font.BOLD,12));
g2.drawString("E(μ",280,177);
g2.setFont(new Font ("Serif",Font.BOLD,12));
g2.drawString("*",300,176);
g2.setFont(new Font ("Serif",Font.BOLD,12));
g2.drawString("|y) =",305,177);
g2.drawString(df.format(d4),335,177);
g2.drawString("Var(μ",280,197);
g2.setFont(new Font ("Serif",Font.BOLD,12));
g2.drawString("*",312,196);
g2.setFont(new Font ("Serif",Font.BOLD,12));
g2.drawString("|y) =",317,197);
g2.drawString(df.format(d8),347,197);
g2.setColor (new Color(0,0,0));
g2.drawString("E(σ",280,217);
g2.setFont(new Font ("Serif",Font.BOLD,12));
g2.drawString("*",300,216);
g2.setFont(new Font ("Serif",Font.BOLD,8));
g2.drawString("2",305,212);
g2.setFont(new Font ("Serif",Font.BOLD,12));
g2.drawString("|y) =",310,217);
g2.drawString(df.format(d3),340,217);
g2.drawString("Var(σ",280,237);
g2.setFont(new Font ("Serif",Font.BOLD,12));
g2.drawString("*",312,236);
g2.setFont(new Font ("Serif",Font.BOLD,8));
g2.drawString("2",317,232);
g2.setFont(new Font ("Serif",Font.BOLD,12));
g2.drawString("|y) =",322,237);
g2.drawString(df.format(d7),352,237);
g2.drawString("E(y) = -0.18",280,257);
g2.drawString("Var(y) = 1.33",280,277);
g2.setColor (new Color(0,0,0));
g2.drawString("F",15,143);
g2.setColor (new Color(79,129,189));
g2.drawString("μ",345,488);
g2.setColor (new Color(0,0,0));
g2.drawString(",",353,488);
g2.setColor (new Color(192,88,77));
g2.drawString("σ",360,488);
g2.setFont(new Font ("Serif",Font.BOLD,8));
g2.drawString("2",371,483);
}
}
source code: normal.java
import java.util.*;
public class normal {
private static Random rnd = new Random(Calendar.getInstance().
getTimeInMillis()+Thread.currentThread().getId());
private static double u;
public static double sampleNormal(double e0, double e1) {
double e2;
e2=Math.pow(e1,(0.5));
u=e2*rnd.nextGaussian()+e0;
return u;
}
}
gamma.java
import java.util.*;
// See the below website, copy and paste the class "Samplers".
// Then modify the code as necessary.
//
// http://vyshemirsky.blogspot.com/2007/11/
// sample-from-gamma-distribution-in-java.html
//
// I express my appreciation for MY STRUGGLE.
In conclusion, the posterior distribution is roughly in such a position that the prior distribution moves from (μ, σ2) to (μ, σ2+0.5) because the posterior distribution is in proportion to the product of the conditional likelihood function and the prior distribution and the posterior distribution are the conjugate distributions. I also presume the assumption that I set the both expectation of σ2 and the variance of σ2 to small numbers reduces the value of both Var(μ*|y) and Var(σ*2|y).
Finally I am happy to assist you in coding and simulating a random process with the MCMC algorithm in JAVA.
I experimentally took a rough guess that the solutions in Fedora might apply to this case and I'd like to express my heartfelt appreciation to several useful websites before I go into the main subject.
1. After trial and error I casually went to Jason Rennie's Home Page and found a link to Numeric-24.2.tar.gz, Numerical Python. I am deeply grateful to him and
the URLs are given below.
http://people.csail.mit.edu/jrennie/python/numeric
http://sourceforge.net/projects/numpy/files
/Old%20Numeric
2. You will need to unzip Numeric-24.2.tar.gz, edit ranf.c, and build Python Numeric. The modification on ranf.c to avoid the error message: "error: conflicting types for 'gettimeofday'" was mentioned by the helpful website given below. The command lines are also given below.
http://osdir.com/ml/python.numeric.general/2005-06/msg00001.html
$ gzcat Numeric-24.2.tar.gz | tar xvf -
$ chmod 777 ./Numeric-24.2/Packages/RNG/Src/ranf.c
$ cd Numeric-24.2 && gedit ./Packages/RNG/Src/ranf.c
<EXAMPLE>
/* int gettimeofday(struct timeval *, struct timezone *); */
$ python setup.py build
# python setup.py install
# reboot
3. You will subsequently need to go to the URL given below, get screenlets-0.1.2.tar.bz2, unzip the source code, and install it. The URL and the command lines are given below.
https://launchpad.net/Screenlets/+milestone/0.1.2
$ bzcat screenlets-0.1.2.tar.bz2 | tar xvf -
$ cd screenlets
# make install clean
4. Afterward you will need to go to GNOME-Look.org, get 76969-RssMini.tar.gz, and install the package on Screenlets using GUI. In reviewing my conduct during the work, I unexpectedly had trouble using RSS mini, consequently edited the line 466 or 467 of RSSMiniScreenlet.py, and specifically deleted '( )' in the line. This modification owes a great deal to the useful website given below and I am deeply grateful to them. The URLs and the command lines
are given below.
http://ubuntuforums.org/showthread.php?t=594681
http://gnome-look.org/content/show.php
/Rss+mini?content=76969
$ gedit $HOME/.screenlets/RssMini/RssMiniScreenlet.py
<EXAMPLE>
class Tooltip ( ):
↓
class Tooltip :
Now you can use RssMini on Screenlets with GUI.
Finally I am happy to assist you to build Python Numeric and install RSS mini which is the Screenlets available from GNOME-Look.org on OpenSolaris build 111.
I fortunately got help from the Mozilla community and other websites. Many thanks for their support. Well, I enter into the main topics.
1. You will need to go to the URL given below and get the package firefox-4.0b3.en-US.opensolaris-i386-pkg.bz2.
http://releases.mozilla.org/pub/mozilla.org/firefox
/releases/4.0b3/contrib/solaris_pkgadd
2. Then you will need to unzip and install firefox-4.0b3.en-US.opensolaris-i386-pkg.bz2 and the command lines are given below.
# bunzip2 -d firefox-4.0b3.en-US.opensolaris-i386-pkg.bz2
# pkgadd -d firefox-4.0b3.en-US.opensolaris-i386-pkg
3. I referred to the useful website given below and could set up Firefox 4.0 beta3. I deeply appreciate what he has done. The URL and the command lines are given below.
http://baian-space.blogspot.com/2009/06/realplayer-
11-gold-with-opensolaris.html
# cp /opt/sfw/share/applications/firefox.desktop /usr/share/applications
# cp /opt/sfw/share/pixmaps/firefox-icon.png /usr/share/pixmaps
4. Then I referred to the helpful website given below and could add the Java plugin and other plugins into the Mozilla plugins. The URL and the command lines are
given below.
http://opensolaris.org/jive/thread.jspa?messageID=454933
# mkdir /opt/sfw/lib/firefox/plugins
# ln -s /usr/java/jre/lib/i386/libnpjp2.so /opt/sfw/lib/firefox/plugins
# cp /usr/lib/firefox/plugins/* /opt/sfw/lib/firefox/plugins
5. After that, you may localize Firefox 4.0 beta3 for your language environment. I referred to the practical websites given below and would like to express my appreciation to them for their work. I actually went to the URL given below, got firefox-4.0b5pre .ja.langpack.xpi, and modified install.rdf in the .xpi file, or more specifically, changed the value of minVersion into 4.0b3pre. Please relax your caution against tentatively taking my native tongue as an example because this way can be applied in many other languages. The URL and the command lines are given below.
http://forum.mozilla.gr.jp/cbbs.cgi?mode=al2&number=43398&rev=&&KLOG=278
http://d.hatena.ne.jp/kakurasan/20080324/p1
http://www1.plala.or.jp/tete009/software.html#JLPAPPLY
http://ftp.mozilla.org/pub/mozilla.org/firefox/nightly/latest-mozilla-central-l10n/
$ cd Downloads
$ mkdir work
$ cd work
$ unzip ../firefox-4.0b5pre.ja.langpack.xpi
$ gedit install.rdf
<EXAMPLE>
<em:minVersion>4.0b3pre</em:minVersion>
$ find -print0 | xargs -0 zip -9 ../ja.xpi -@
Now you can localize Firefox 4.0 beta3 for your language environment, adding on ja.xpi to the language pack in Firefox and setting general.useragent.locale, which is the entry in about:config, of ja-JP.
Finally I am happy to assist you to install and set up Firefox 4.0 beta3 on OpenSolaris build 111.
The main purpose of this article particularly focuses on OpenSolaris but looking at the matter objectively, the background of this article is under a debt to the Linux communities. I am deeply grateful to the Linux communities.
1. You will need to go to the URL given below and get the package RealPlayer11Gold-x86.tar.bz2.
http://www.real.com/realplayer/solaris
2. You will need to unzip RealPlayer11Gold-x86.tar.bz2 and the command lines are given below.
# mkdir /opt/real
# cp RealPlayer11Gold-x86.tar.bz2 /opt/real
# cd /opt/real
# bzcat RealPlayer11Gold-x86.tar.bz2 | tar xvf -
3. I referred to the useful website given below, YoLinux Tutorial and I express my gratitude for his or her effort. We will accordingly need to set up RealPlayer 11, or more specifically, add nphelix.so and nphelix.xpt o mozilla plugins and set $HELIX_LIBS. The URL and the command line are given below.
http://www.yolinux.com/TUTORIALS/LinuxTutorialMozillaConfiguration.html
# ./postinst/postinst.sh
4. You may subsequently localize RealPlayer 11 for your language environment. I also referred to the helpful article given below, bend_tail and I sincerely
give thanks to the contents. We can consequently choose the language environment among German, Spanish, French, Italian, Japanese, Korean, Brazillian Portuguese, Simplified Chinese, and Traditional Chinese. I provisionally take my native tongue as an example. ;The URL and the command lines are given below.
http://d.hatena.ne.jp/bend_tail/20071107/1194397835
# ln -s /usr/lib/RealPlay/share/locale/ja/player.mo /usr/share/locale/ja/LC_MESSAGES/realplay.mo
# ln -s /usr/lib/RealPlay/share/locale/ja/widget.mo /usr/share/locale/ja/LC_MESSAGES/libgtkhx.mo
Finally I am happy to assist you to install and set up RealPlayer 11 on OpenSolaris build 111.
I tentatively replaced a USB printer to the network printer for the convenience about two years ago because it had a reasonable price, below $250, considering it was an all-in-one printer and wireless LAN was available for connecting it to several other machines.
There were, however, two problems in addition to the malfunction of the CUPS drivers, such as PM-T960. One of the problems was the error message that 'libltdl. so.3 is needed by pipslite-1.4.0-5.i386' when I tried to install pipslite-1.4.0-5.i386.rpm. The other was the error message that "libtool: link: cannot find the library '../libltdl/libltdl.la' or unhandled argument '../libltdl/libltdl.la'" when I tried to build pipslite_1.4.0-5.tar.gz.
The problems were somehow fixed after I had found the driver of Epson PM-T960, Stylus photo RX560, or RX690 was compatible with Epson PM-A840S.
The URL and the command line was given below.
http://avasys.jp/eng/linux_driver/download/lsb/epson-inkjet/escpr/
# rpm -ivh epson-inkjet-printer-escpr_1.0.0-1lsb3.2.x86_64.rpm
You might need to select the driver of PM-A840S using the CUPS interface to print with Epson PM-T960, Stylus photo RX560, or RX690 after that.
Finally I am happy to assist you to use the printers compatible with PM-A840S on Fedora 13 x86_64.
1 How to set up MPlayer plugins
1.1 OpenSolaris doesn't have SUNWfirefox-devel, which is required when building mplayerplug-in-daily.tar.gz, so we might need to install firefox-3.1b3.en-US.open
solaris-i386-pkg.bz2, which includes SUNWfirefox, SUNWfirefox-devel, and SUNWfirefox-bookmark. We can get the package from the URL given below.
http://ftp.mozilla.org/pub/mozilla.org/firefox/nightly/contrib/3.1b3-candidates/build1/
1.2 You might need to uninstall firefox, reinstall the relative packages, and reboot to install firefox-3.1b3.en-US.opensolaris-i386-pkg.bz2. The command lines are given below.
# pkg uninstall SUNWgnome-help-viewer
# pkg uninstall SUNWcodeina
# pkg uninstall SUNWipkg-gui
# pkg uninstall SUNgnome-python-extras
# pkg uninstall SUNWfirefox
# pkg install SUNWgnome-help-viewer
# pkg install SUNWcodeina
# pkg install SUNWipkg-gui
# pkg install SUNgnome-python-extras
# reboot
1.3 You can install firefox-3.1b3.en-US.opensolaris-i386-pkg.bz2. The command lines are given below.
# bunzip2 -d firefox-3.1b3.en-US.opensolaris-i386-pkg.bz2
# pkgadd -d firefox-3.1b3.en-US.opensolaris-i386-pkg
1.4 Then I referred to the useful website given below and could install MPlayer. I express my heartful thanks to homeunix.com and the command lines are given below.
http://solaris.homeunix.com/?q=node/24
# pkg set-authority -O http://ips.homeunix.com:10906 homeunix.com
# pkg refresh --full
# pkg install MBLmplayer
1.5 Next you might need to install mplayerplug-in-daily.tar.gz. We can get the package from the URL given below and the command lines are given below.
http://mplayerplug-layerplug-in.sourceforge.net/download.php
$ gzcat mplayerplug-in-daily.tar.gz | tar xvf -
# pkg install SUNWgnome-common-devel
# ./configure
# make -i install clean
1.6 Now we can play wmv files using MPlayer plugins on Firefox and confirm we added mplayerplug-in to mozilla plugins.
2 How to use the CUPS drivers in Gutenprint
2.1 Second we confirm CUPS and the relative packages were installed or install them using a
package manager if they weren't installed.
2.2 We might need to install gutenprint-5.2.6.tar.bz2 and can get the package from the URL given below. The command lines are also given below.
http://sourceforge.net/projects/gimp-print/files/
# bzip2 -dc gutenprint-5.2.6.tar.bz2 | tar xvf -
# cd gutenprint-5.2.6
# ./configure --enable-cups-ppds
# make install clean
# reboot
2.3 Then we might need to enable CUPS and the command lines are given below.
# print-service -s cups
2.4 Now we can use the CUPS drivers in Gutenprint, for example Epson PM-T960 compatible with Epson Stylus photo RX595, RX680 from the
URL http://localhost:631/.
Finally I am happy to assist you to set up MPlayer plugins and use the CUPS drivers in Gutenprint on OpenSolaris build 111.
I have reluctantly canceled the RAID array on Inspiron 531s recently because I unfortunately had no option but to realize the latest updates
for Fedora 13, such as the alternation of Dracut, mapping, and mdraid instead of dmraid, didn't recognize NVIDIA RAID array. It however seemed
I had also better upgrade from FreeBSD 7.1 or the older version, which had been already installed on the RAID drive, to the latest FreeBSD 8.1 on the non-RAID drive at the same time if I was going to do it. That is why I came to grips with the installation of FreeBSD 8.1 several times.
First the X server failed to start after installing FreeBSD 8.1 on the machine with NVIDIA video card. Therefore I previously downloaded NVIDIA-
FreeBSD-x86_64-256.44.tar.gz in a FAT32 partition and installed the driver in the CUI editor. The command lines are given below.
# tar xzf NVIDIA-FreeBSD-x86_64-256.44.tar.gz
# cd NVIDIA-FreeBSD-x86_64-256.44
# make install clean
# nvidia-xconfig
Second I couldn't see the CUPS interface at http://
localhost:631/. Therefore I reinstalled cups-base and cups-client and installed cups-image from ports.
After that I edited cupsd.conf in /usr/local/etc/cups to set the authentication. The command lines are given below.
# cd /usr/ports/print/cups-base
# make deinstall && make install clean
# cd ../cups-client
# make deinstall && make install clean
# cd ../cups-image && make install clean
Third I tried to install openoffice.org-3 from ports and the size of /usr was 23GB. It actually was not little enough. To put it concretely, it was enough to make openoffice.org-3 but not enough to install openoffice.org-3. Therefore I temporarily moved some directories into the home directory and made room for installing openoffice.org-3 in /usr. The size of them was about 1.2GB, so the size of /usr, which was
about 24GB, might be enough to install openoffice.org-3.
Finally I am happy to assist you in solving these various problems on FreeBSD 8.1 amd64.
Ich erlebt, dass Audio-Datein mit dem Real Player nach dem Wiedergabe von Flash-Datein nicht wiedergegeben werden konnte. Tatsächlich konnte ich BBC World Service mit dem Real Player nicht anhören, nachdem ich ZDF
heute-Sendung mit dem Flash Player angesehen hatte.
Die Weise, wie ich das besagt Problem vermied, war ein Neustart von PulseAudio und ich gab die nachstehende Kommandozeile nach dem Schliessen des Browser ein.
$ pulseaudio -k
Dann drückte ich nur Alt+F2 aber danach bestätigte ich, dass es gut ging, auch wenn ich diese Tasten nicht drückte. Immerhin war das gesagt Problem mit der gesagt Weise gelöst.
Aber danach stellte ich fest, dass ich nur an den Browser zu schliessen brauchte, um Audio-Datein mit dem Real Player nach dem Wiedergabe von Flash-Datein oder der Verwendung von VLC media player zu abspielen und dass ich die gesagt Kommandozeile zu eingeben brauchte, um den VLC media player zu verwenden, nachdem ich Audio-Datein mit dem Real Player abgespielt hatte.
Schliesslich freue ich mich, Ihnen bei der Lösung das Problem über PulseAudio auf Fedora 12 zu unterstützen.
It took five days with occasional rests to solve the problems approximately and it was never out of my mind if I may be allowed a little exaggeration. I'd like to express my appreciation for the various websites referring to the problems mentioned above.
First I used pkg_add to install Gnome2 and dependencies, deleted gdm from the system, and installed gdm from ports. Besides that, to change the login background screen, I replaced background-default.jpg which was in /usr/X11R6/share/pixmaps/backgrounds/gnome.
Second one of the useful websites referring to installing OpenOffice for FreeBSD is given below.
http://porting.openoffice.org/freebsd/
The command line to install the package after downloading OOo_3.1.1FreeBSD80X86_64_install_ja.tbz is given below.
# pkg_add -f OOo_3.1.1FreeBSD80X86_64_install_ja.tbz
Actually I had tried to build openoffice.org-3 from ports but the size of /usr I adopted was not enough and then switched the way to install openoffice.org-3 from ports to using pkg_add.
Third I built multimedia/gstreamer-plugins-all from ports to play wma and asx files. The command line to build the package is given below.
# make -i install clean
Actually I had built audio/gstreamer-plugins-lame, audio/gstreamer-plugins-mad, and audio/gstreamer-plugins-wavpack from ports but gstreamer-plugins-bad was missing from the indispensable packages to listen to BBC World Service and RFI and then switched the way to build them from picking up them one by one to building multimedia/gstreamer-plugins-all from ports. Consequently, I could listen to the internet radio broadcasting as given above.
Fourth, after building compiz and dependencies from ports, I went to System->Preferences->Startup Applications->Startup Programs, added Startup Programs such as Compiz and Emerald, and edited their commands. The examples are given below.
Name: Compiz
Command: compiz --replace gconf
Name: Emerald
Command: emerald --replace
Plugin List includes core, dbus, decoration, glib, move, place, resize, scale, and switcher.
Fifth I referred to the useful website mentioned below.
http://www.mail-archive.com/freebsd-bluetooth@freebsd.org/msg00661.html
I am very much indebted to the website for their useful suggestion. Reverting to the subject, I added the command lines as given below to /boot/loader.conf.
netgraph_load="YES"
ng_ubt_load="YES"
Besides that, I added the command lines as given below
to /etc/rc.conf.
hcsecd_enable="YES"
devd_enable="YES"
By default, ng_ubt recognized the bluetooth device, ubt0, in Thinkpad SL400 and also another bluetooth device, ubt1,
such as BTMicroEDR2X. Then I made connection.sh according to the website mentioned above for connecting Bluetooth PAN.
# vi connection.sh
#!/bin/bash
ifconfig tap0 create mtu 600
btpand -a 00:00:00:00:00:00 -d ubt0 -s NAP -i tap0
#Put the MAC address of our bluetooth device,
#such as a pocket PC or a smart phone,
#into 00:00:00:00:00:00
dhclient tap0
# chmod a+x connection.sh
After pairing the bluetooth device, I could connect Bluetooth PAN on FreeBSD 8.0 amd64. The command line to connect Bluetooth PAN is given below.
# sh connection.sh
Finally I will be happy to assist you in solving these various problems on FreeBSD 8.0 amd64.
It took eight days at a stretch to solve the problems mentioned above. As many people have mentioned in various places, I will also frankly describe how to deal with these matters.
First the background image such as default.jpg or constantine.png is always displayed by default. The reason why is that Wallpapoz Autostarter works in startup programs. Therefore we have to turn off wallpapoz-autostart to set the background image.
Second some screenlets such as Weather and RssMini require the numerical extension to Python. The command line to work the widgets appropriately is given below.
# yum install python-numeric*
Third Open PGP Key Management haven't worked well in the Japanese language environment since Enigmail 0.97a. To put it concretely, I couldn't set owner trust and deal with imported keys but import keys from files on Open PGP Key Management window in the Japanese language environment. However, in the English language environment, Open PGP Key Management works well and there seems to be no problems. One of the
solutions is to select the English language environment on gdm.
Fourth I could install NVIDIA-Linux-x86_64-190.42-pkg2.run on Fedora 12 on Dell Inspiron 531s but couldn't install it on Fedora 12 on Lenovo Thinkpad SL400 by default. One of the useful websites in this case is given below.
http://linuxsoftwareblog.com/blog/?p=232
Accordingly we might need to edit grub.conf and add nouveau.modeset=0 and vga=0x318 to kernel parameters for the time being.
# vi /boot/grub/grub.conf
<EXAMPLE>
kernel /vmlinuz-2.6.31.5-127.fc12.x86_64 ro root=/dev/mapper/VolGroup00-LogVol01 nomodeset Lang=ja_JP.UTF-8 KEYBOARDTYPE=pc KEYTABLE=jp106 rhgb quiet nouveau.modeset=0 vga=0x318
The command line after that is given below.
# ./NVIDIA-Linux-x86_64-190.42-pkg2.run --kernel-source-path /lib/modules/$(uname -r)/build
Finally I will be happy to assist you in solving these various problems on Fedora 12.
First we need to install Sounds for Gnome, such as gnome-audio-2.22.2-4.fc11.noarch and ascertain login.wav is stored in the directory /usr/share/sounds.
Second we go to System>Preferences>Personal>Startup Applications>Startup Programs, select Gnome Login Sound, and edit its command.
The initial state is given below.
/usr/bin/canberra-gtk-play --id="desktop-login" --description="GNOME Login"
It needs to be modified as given below.
/usr/bin/canberra-gtk-play -f /usr/share/sounds/login.wav --description="GNOME Login"
Third we can hear login.wav instead of desktop-login.ogg when we login again.
Finally I will be happy to assist you in customizing the login sound on Fedora 11.
One of the solutions is to build gnome2 and dependencies from ports, which some web sites show. So I didn't install Gnome2 and dependencies
but Xorg and dependencies from DVD-R.
First I updated ports using portsnap.
# portsnap fetch
# portsnap extract
Second I installed Gnome2 and dependencies from ports.
# cd /usr/ports/x11/gnome2
# make install clean
It required more than 10 hours and less than 24 hours and there were a lot of error messages
during building gnome2. I used pkg_add to deal with the error messages relative to the installation of some of the packages.
# pkg_add -r THE_PACKAGE_NAME
However, I didn't use pkg_add to install pulseaudio and gdm. Please make sure that you install pulseaudio and gdm from ports through building gnome2 and dependencies.
Third the size of /usr I adopted was about 16GB but it was not enough when I built jdk16 and openoffice.org-3 after having built gnome2. Therefore, I removed all files in /usr/ports/distfiles when I built openoffice.org-3.
# cd /usr/ports/distfiles
# rm -rf *
Finally I will be happy to assist you in solving the problems related to pulseaudio and gdm on FreeBSD 7.2.
In the beginning I refered to the web site mentioned below to solve the problem.
http://www.k13i.com/~koya/notepc.html
I'd like to express my appreciation to the web site mentioned above. It is, however, written in my native language, Japanese so you might need to use something like a translator, such as Google translate but I will
describe the gist of its content and support you in solving the problem.
The problem was that the error message "alsamixer: function snd_ctl_open failed for default: No such device" was shown on the screen and that alsamixer wasn't available on Debian 5.0 when we
started alsamixergui with YMF-744B. This might be because the firmware for YMF-744B wasn't installed and because the DFSG adhered to a strict interpretation of FOSS.
According to the web site mentioned above, we need to go to ALSA project homepage,
http://www.alsa-project.org/main/index.php/Main_Page
and download alsa-firmware-1.0.20. After then we need to install alsa-firmware. The command lines are given below.
# tar jxvf alsa-firmware-1.0.20.tar.bz2
# cd alsa-firmware-1.0.20
# ./configure
# make
# make install
# alsaconf
After configuring ALSA through alsaconf, we could confirm alsamixer was available on Debian 5.0.
Finally, I will be happy to assist you in setting up alsamixer with YMF-744B on Debian 5.0.
Il y avait pleusieurs solutions variables. Je n'ai pas pu lire le fichier wmv sur France2.fr avec Gnome MPlayer sur Firefox 3.5 après le 29 juillet alors que j l'ai pu lire avec Gnome MPlayer indépendant. En plus il y a eu un message d'erreur quand j'ai compilé et installé mplayerplug-in-3.55.tar.gz. C'est pourquoi j'ai utilisé MPlayer et mplayerplug-in-daily.tar.gz. En bref, nous pouvons maintenant compiler et installer
mplayerplug-in-daily.tar.gz avec les préférences par défaut de Fedora 11, MPlayer peut être utilisé sur le navigateur web par le plugin, et mplayerplug-in-0.4.xpi n'était pas disponible sur Firefox 3.5 en juillet 2009 à cause du problèm avec la mise à jour de le plugin.
Je me suis référé à http://mplayerplug-in.sourceforge.net/. Les commandes lignes que j'ai utilisé sont montrés ci-dessous.
$ tar -xzvf mplayerplug-in-daily.tar.gz
$ cd mplayerplug-in
$ ./configure
$ make
$ make install
J'ai specifié le pilote vidéo xv et le pilote audio pulse sur MPlayer pour lire un fichier wmv sous Fedora 11.
Enfin je vous souhaite de réussir à lire un fichier wmv sur Firefox sous Fedora 11.
J'ai pensé arbitrairement que il fallait installer VLC media player, le plugin, et les paquetages relatifs. Je n'ai en fait pas pu lire le fichier wmv du journal télévisé de France 2 avec un lecteur multimédia par défaut de Fedora 11, c'est-a-dire Totem, avant 9 juillet 2009, tandis que c'était bien que je le pouvais lire avec VLC Media Player. Je me suis aperçu après que France 2 recommandait une installation de la dernière version de MPlayer. Il y a eu plusieurs solutions et j'utilise actuellement MPlayer à lecture de la vidéo. C'est parce que il peut cesser temporairement de jouer la vidéo en streaming et que il y a un progress slider disponible sur Firefox. Je confirme seulment que maintenant nous ne pouvons pas déplacer librement le slider.
Les URLs sont http://jt.france2.fr/20h/ et http://videojts.francetv.fr/player/aide/index.php et vous trouvez la capture d'écran ci-dessous. La figure 1 montre la capture d'écran du journal télévisé avec VLC Media Player que n'a pas le progress slider disponible sur Firefox. Il ne peut donc pas cesser temporairement de jouer la vidéo en streaming.
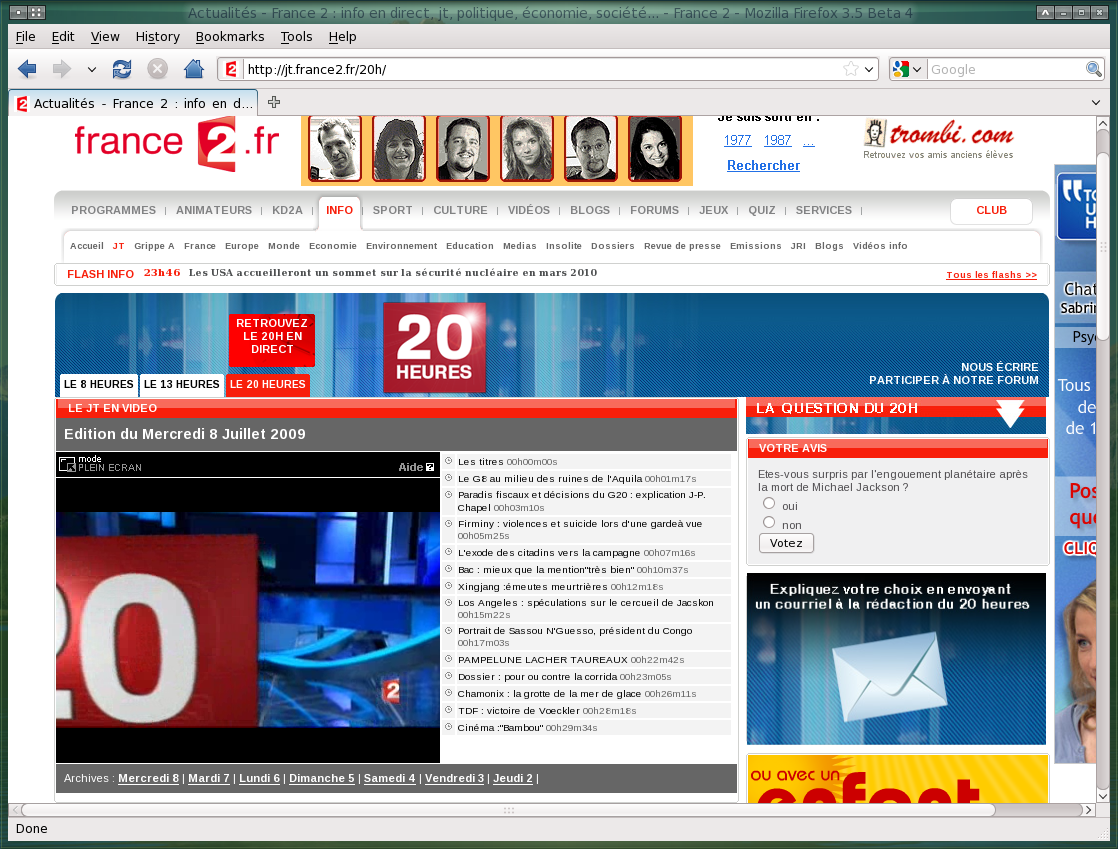
Figure 1 Le journal télévisé avec VLC Media Player
La figure 2 montre la capture d'écran du journal télévisé avec MPlayer et vous pouvez confirmer que il y a le progress slider disponible sur Firefox au coin gauche en bas de la capture d'écran.
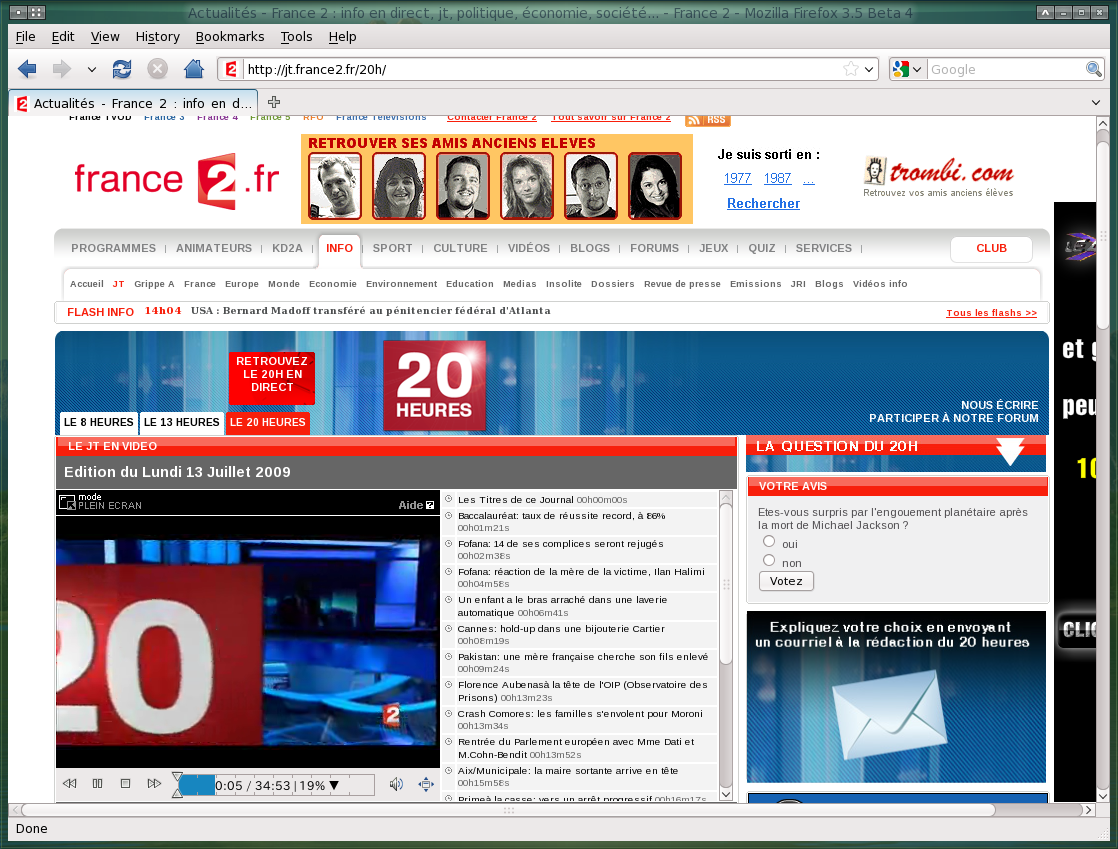
Figure 2 Le journal télévisé avec MPlayer
Enfin je vous souhaite de réussir à regarder les journaux télévisés de France 2 sous Fedora 11.
OpenSolaris installs Grub in MBR. Grub in MBR, however, interferes with installing Windows Vista SP2. Normally installing Windows Vista SP2 demands using Windows Boot Manager when we choose an operating system.
Firstly, we need to boot OpenSolaris using Windows Boot Manager. Therefore we confirm Fdisk information for device /dev/rdsk/c3t0d0p0 after installing FSWpart and FSWfsmisc. c3t0d0p0 is an example and dependent on each environment. The command lines are given below.
# prtpart
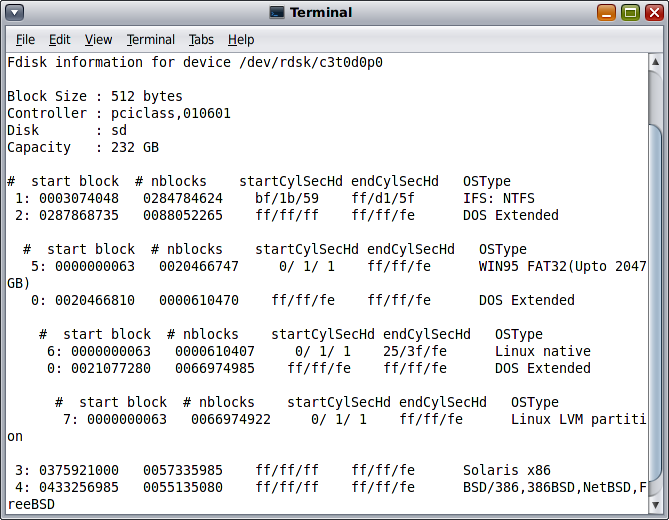
Figure 1 Fdisk Information
# prtpart /dev/rdsk/c3t0d0p0 -ldevs
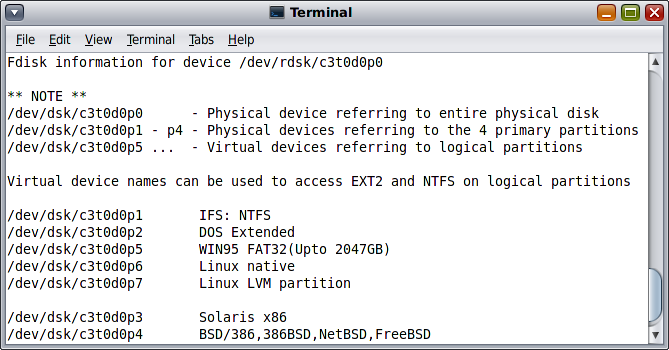
Figure 2 Virtual Device Names
After confirming a virtual device name of Solaris x86, we create the boot image of the OpenSolaris using the dataset definition. The command line is given below.
# dd if=/dev/rdsk/c3t0d0p3 of=osol.bin bs=512 count=1
After then we copy osol.bin in the directory on FAT32 and Windows C drive. For example, C:\osol.bin.
Next we use Windows console which requires administrative privilege. The command lines are given below.
>bcdedit /copy {ntldr} /d "OpenSolaris"
>bcdedit /set {GUID} device partition=C:
>bcdedit /set {GUID} path \osol.bin
>bcdedit /displayorder {GUID} /addlastAfter reboot and the selection of Windows through Grub menu we can boot OpenSolaris using Windows Boot Manager.
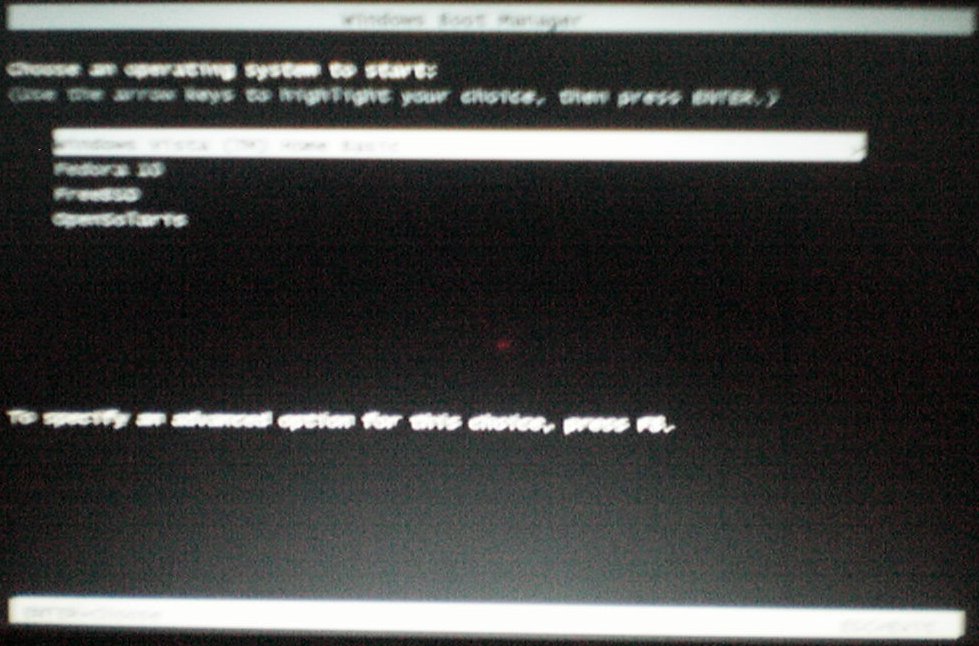
Figure 3 Windows Boot Manager
Secondly, we designate NTFS partition including Windows Vista as an active partition, using for example GParted and so on.
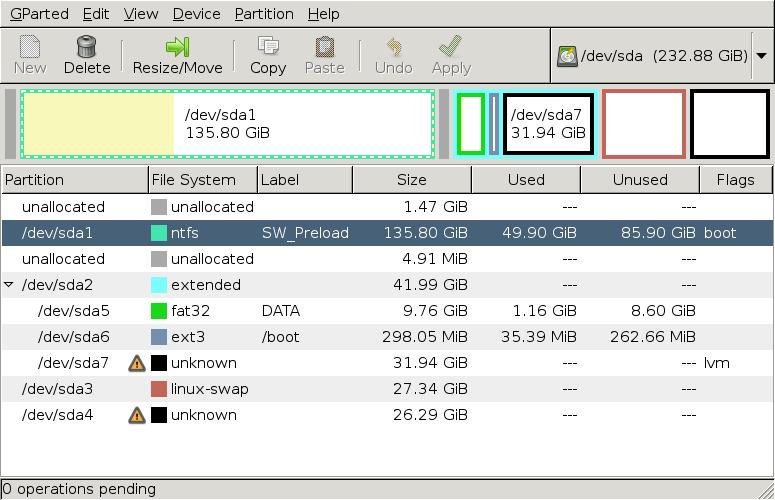
Figure 4 GParted Partition Table
Figure 5 Active Partition
After then we recover Windows MBR using Vista Recovery Console. The command line is given below.
>bootrec /FixMbr
Thirdly, after installing Windows6.0-KB948465-X86.exe, we have applied Windows Vista SP2 on a dual boot system including OpenSolaris.
Finally, I will be happy to assist you in installing Windows Vista SP2.
1999年発売のFMV-DESKPOWER C2/507の
DVD-ROMドライブが故障してから約1年半が過ぎよう
としていた。メーカーのテクニカルサポートから交換
部品の在庫がないと言い渡され、その半年後サポート
を打ち切る旨のメールが配信された。
BUFFALO、IO-DATAの対応情報によれば、
採用ドライブがソニーNECオプティアーク、パイオニア
製の場合動作報告がなく、パナソニック製の場合に
辛うじて動作報告がある現状だった。
こういうケースでは、古いPCは時間が経てば
経つほど部品が生産完了になり、早めに手を打つ
必要があることを認識していただけるだろう。
但し、パナソニック製のドライブにしてもXPのSP2
に対応したDVDドライブであり、殻付DVD対応である
ことからトレイの大きさが最後まで懸念材料のひとつ
だった。
当方の使用状況はWindows98SEからWindowsXP
SP2にバージョンアップ済みの状態で、OSの問題を
クリアしていたことを鑑み、DVR-AM16CVでの
動作報告はなかったが、これなら行ける可能性が
あるかもしれない、うまくいかなければSR-8585-B
に互換するドライブを海外を含めて広く探して調達
すれば良いかとの漠然とした考えを抱いていた状況
だった。
結論から言うと、FMV-DESKPOWER C2/507の
SR-8585-Bが故障した場合、OSがXPのSP2ならば
DVR-AM16CVのベゼルの蓋を取り外して、SR-8585-B
のベゼルの突起部をDVR-AM16CVのトレイの前部に
瞬間接着剤で張り付ける程度の作業を厭わなければ、
SR-8585-Bの代わりにDVR-AM16CVを使用することは
可能である。
しかしOSがXPのSP2のためリカバリディスクを使用して
再度Windows98SEをインストールすることは避けた方が
良いだろう。
実際動作を検証したのは、DVDブートでKNOPPIXが
起動するかとWindowsのデバイスマネージャーでDVD
ドライブに対するドライバが正常に動作しているかの
2点に単純化したものになったが、どちらも問題は
なかった。
結果として、SR-8585-Bを使用していた頃は
DVD-ROMの読み込みのみ可能だったが、DVR-
AM16CVに交換したことにより、DVD-RW, DVD-
RAMの書き込みが可能になったことを確認し、
これは光学ドライブのアップグレードと言っても
良いだろうとの思いを抱いた。
内蔵DVDドライブが故障したPCを修理する必要性に
かられた方にこの記事が参考例の1つとして役立つ
ことを祈るばかりである。
A few months ago I experienced the hard disk drive was corrupted unfortunately and the blue screen appeared while I was working in the office. Because of breakdown within the guarantee period, I didn't have to take on the responsibility. However, I have been faced with the
necessity to deal with an abrupt hardware failure. This is why I try to configure RAID 1 on my nForce 430 (MCP61).
First, I started in to enable RAID globally and on the individual SATA ports from Serial-ATA Configuration window in the System BIOS.
![]() Figure 1 Serial-ATA Configuration window
Figure 1 Serial-ATA Configuration window
After creating the RAID array using the RAID BIOS, MediaShield Utility window shows the RAID array healthy.
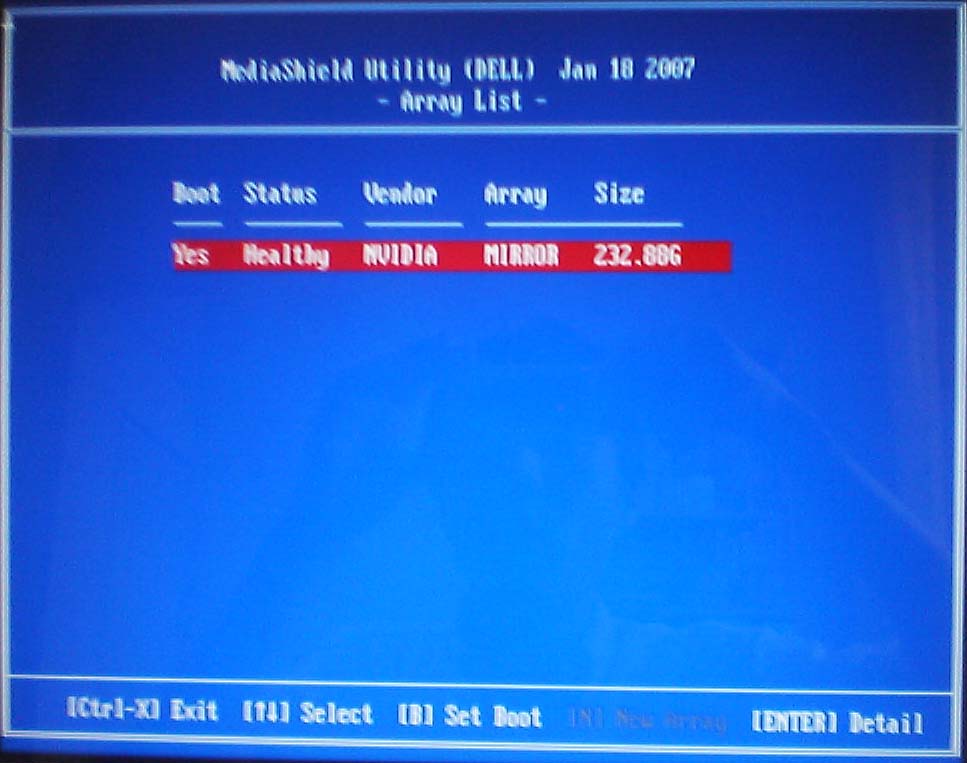
![]() Figure 2 MediaShield Utility
Figure 2 MediaShield Utility
The RAID prompt shows the RAID array healthy as a matter of cource.
![]() Figure 3 RAID Prompt
Figure 3 RAID Prompt
You can rebuild the array from the Array Detail screen.
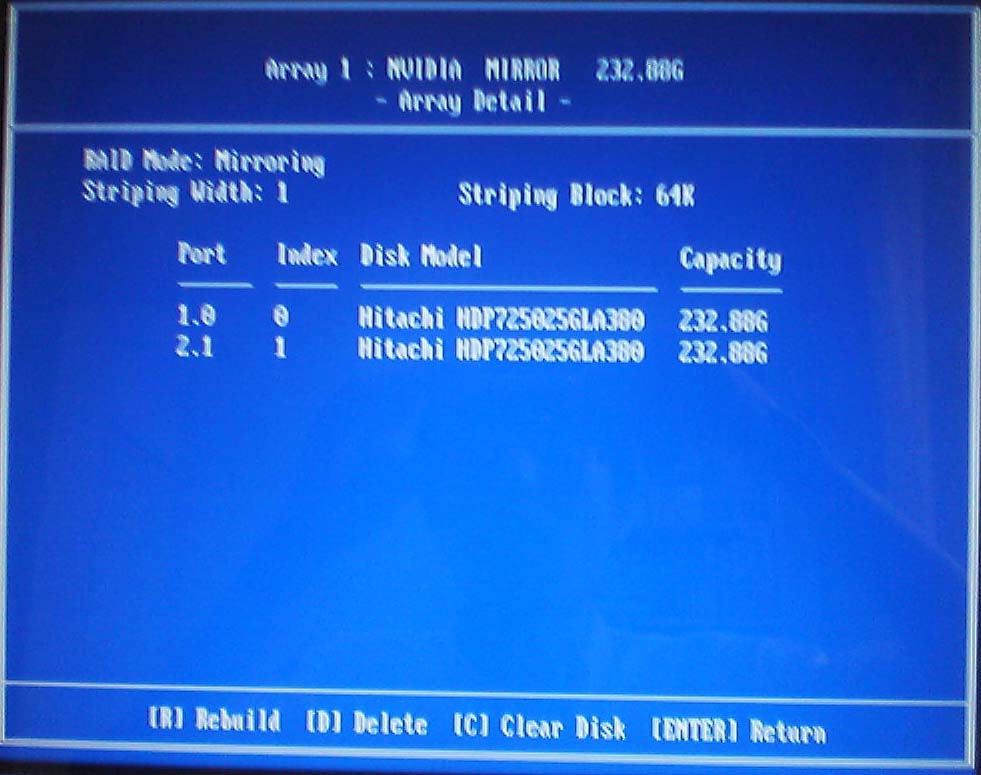
![]() Figure 4 Array Detail Screen
Figure 4 Array Detail Screen
You can use the arrow keys to select the disk.
![]() Figure 5 Array Detail-1.0 selected
Figure 5 Array Detail-1.0 selected
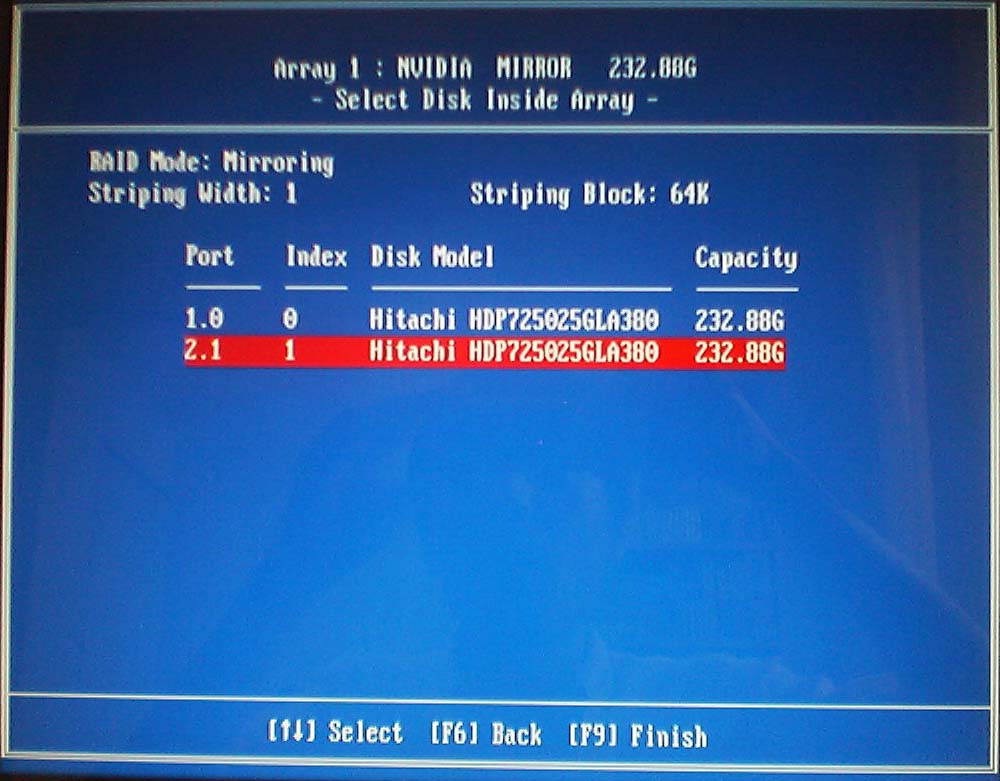
![]() Figure 6 Array Detail-2.1 selected
Figure 6 Array Detail-2.1 selected
![]() Figure 7 Rebuild Array Prompt
Figure 7 Rebuild Array Prompt
During the rebuild MediaShield Utility window shows the RAID array rebuild.
![]() Figure 8 MediaShield Utility
Figure 8 MediaShield Utility
In addition, the RAID prompt shows the RAID array rebuild.
![]() Figure 9 RAID Prompt
Figure 9 RAID Prompt
When you install Fedora 10 on the RAID array, you won't see /dev/sdax but /dev/mapper/nvidia_xxxxxxxx.
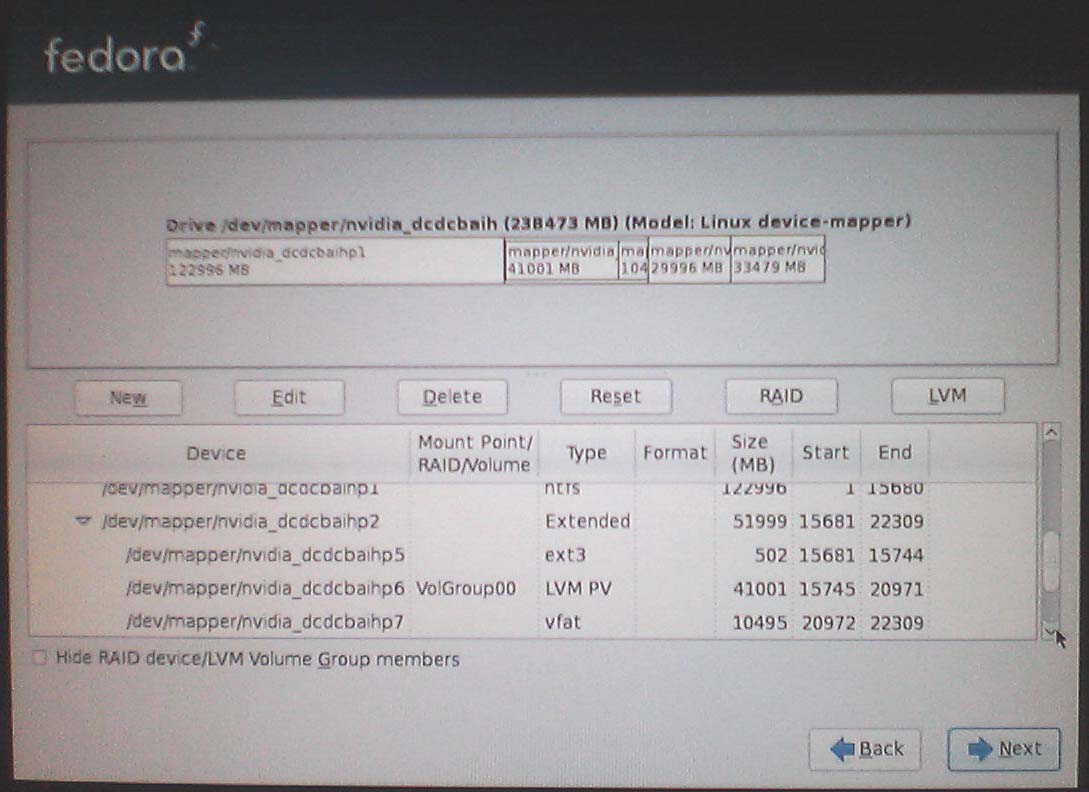
![]() Figure 10 Fedora Select Partition window
Figure 10 Fedora Select Partition window
When you install FreeBSD 7.1 on the RAID array, you won't select adx but ar0.
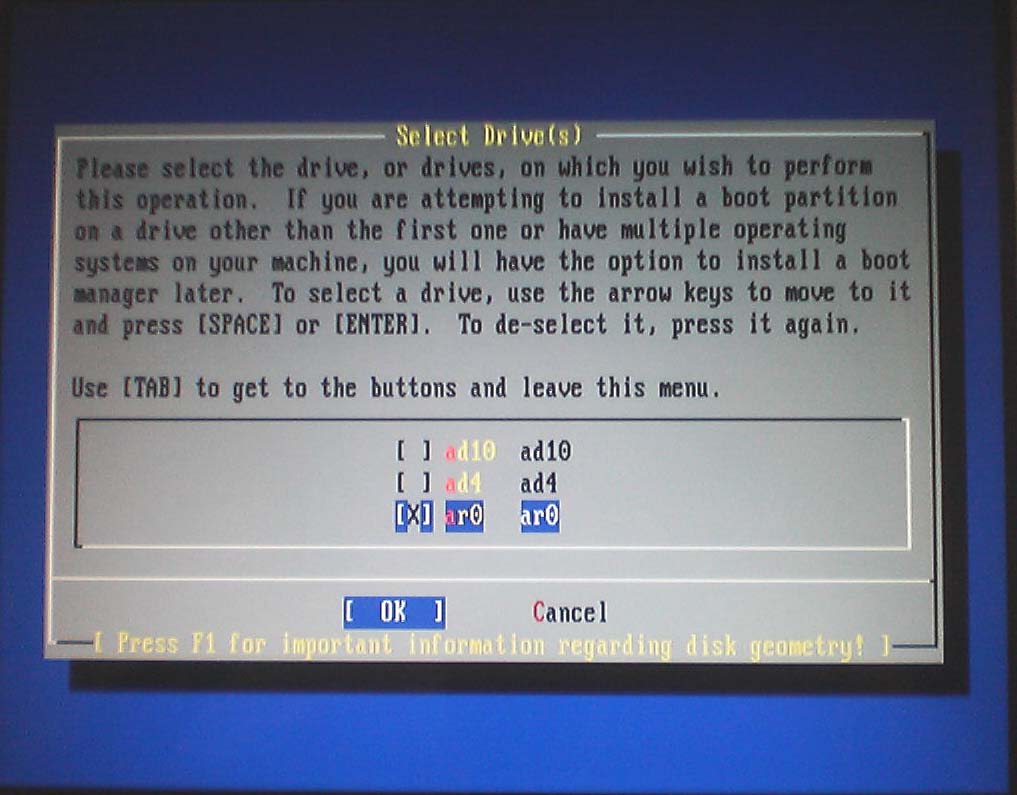
![]() Figure 11 FreeBSD Select Drive window
Figure 11 FreeBSD Select Drive window
Finally, we would confirm a part of RAID 1 performance using HDD benchmark software.
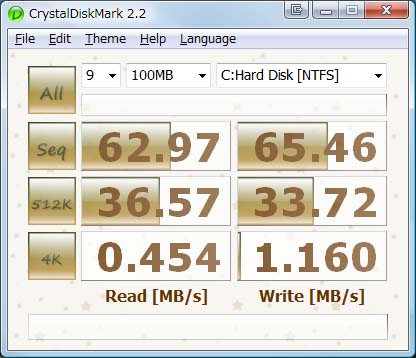
![]()
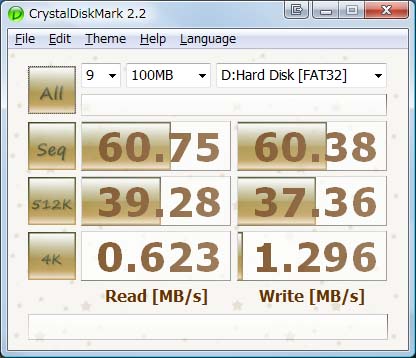
![]() Figure 12
Figure 12 ![]() Figure 13
Figure 13
Figure 12 shows the case of the RAID array including several operating systems and Figure 13 shows the case of the RAID array not including operating systems.
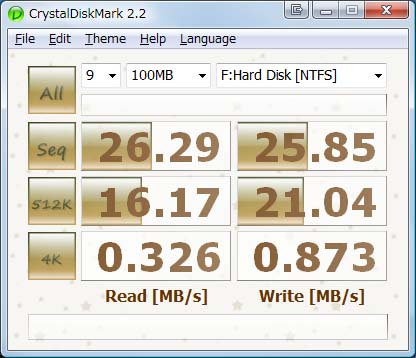
![]() Figure 14
Figure 14
Figure 12 and Figure 13 shows the case of the rotational speed which is 7200rpm and Figure 14 shows the case of the rotational speed which is 5400 rpm and the case of a single drive not including operating systems.
In the beginning I referred to http://bluez.sourceforge.net/contrib/HOWTO-PAN and
http://blog.myfenris.net/?tag=bluetooth-pan.
I'd like to express my appreciation to the web sites mentioned above.
Now I am writing this article intended for users who can set up Bluetooth PAN on Windows though this is the first time that they set up Bluetooth PAN on Fedora 10.
1. You will need to make ifcfg-bnep0.
$ su
# vi /etc/sysconfig/network-scripts/ifcfg-bnep0
DEVICE=bnep0
BOOTPROTO=DHCP
ONBOOT=no
2. You will need to make connection.sh according to your convenience for connecting Bluetooth PAN.
# vi connection.sh
#!/bin/bash
modprobe bnep
pand --connect 00:00:00:00:00:00
# Put the MAC address of your bluetooth device,
# such as a pocket PC or a smart phone,
# into 00:00:00:00:00:00.
ifconfig bnep0
ifup bnep0
# chmod a+x connection.sh
3. You will need to open the Internet Sharing Connection after pairing the bluetooth device, such as a pocket PC or a smart phone, with your Laptop PC. Regarding pairing, see other useful web sites.
4. You will need to go to System -> Administration -> Network, double click on the bnep0, set the bnep0 to start on boot, quit Network Configuration and reboot.
5. Execute connection.sh.
$ su
# ./connection.sh
When I executed connection.sh twice, I could connect Bluetooth PAN on Fedora 10.
Finally, I will be happy to assist you in setting up Bluetooth PAN on Fedora 10.
Windows7 beta 64bit に関する動作報告の続編になる。75%程度、Vista 32bit の状態を再現することが可能になったと言ったらお叱りを受けるだろうか。
32bitアプリケーションに関し、Firefox 3.0.5、Thunderbird 2.0.0.19 は正常に動作していることを確認する。
Inspiron531sに付属していたRoxio Creator DE 9.0.117、PowerDVDに関し、インストール時エラーを示すウインドウが前者では立ち上がることもあったが正常に起動する段階までは確認した。
Google Desktopについては、MSDOSにて、
# GoogleDesktopSetup.exe /force
を実行することにより、インストール及び起動が可能になることを確認する。
他方、ObjectDesktop、Ultramonについては、今後の対応待ちの状態にあるが、後者に関しレジストリを変更すれば使用可能であることを確認する。
さらにNVIDIAのドライバに関し、181.20_geforce_winvista_64bit_international_whqlが正常にインストールされ、又動作したことを補足する。
最後になりましたが、この記事が読者の皆様のお役に立てることを祈る次第です。
では。
Windows7 beta, 64ビットを試す機会に恵まれ、
ここに経緯を記す。具体的にはドライバとアプリ
の動作状況になる。
IEは32ビット版と64ビット版の2種類がインスト
ールされ、Flash, Javaのアプレットは32ビット版の
IEで表示される運びになる。
Epson, PM-T960のプリンタドライバはインスト
ール時にエラーが生じるが、Windows7のコント
ロールパネル>プリンターの追加>ネットワーク、
ワイヤレスまたはBluetoothプリンターを追加
する(W)にて、テスト印刷が可能な状態になる。
ウイルス対策ソフトに関し、ノートン インター
ネットセキュリティ2008のインストールではエラー
が生じるが、インターネットセキュリティ2009にて
インストールが可能になり、現在のところ動作に
不具合はない。
Office Professional 2007に問題はなく、同様に
FrontPage 2000のインストールに関しても問題は
なかった。又、古いがPhotoshop Elements 2.0の
インストールに関しても問題は生じていない。
この記事が皆様の問題解決に資することを
祈るのみである。
では。
I have not been able to listen to BBC World Service on RealOne Player for Pocket PC Version 2.0.0.28 since a latter half of December 2008. This reason is an alternation of Real Media format, in fact, livenews_v8.ra has been changed into live_news_au_nb.ram since last December.
The first step in solving this problem is to install TCPMP on our smart phone or pocket PC. Google is a great help to install TCPMP.
After installation, go to Option>Settings>Select Page>File Associations, and check the Windows metafiles (ASX,WMX,MVX,WAX) box and other relative boxes.
When you opened live_news_au_nb.asx on TCPMP and the error message appeared, such as Unknown file format!, you might need to rewrite live_news_au_nb.asx.
<asx version = "3.0" >
<entry>
<ref href="http://www.bbc.co.uk/worldservice/meta/tx/nb/live/www17.asx" />
</entry>
</asx>
This href has a suitable time. Now I write down this article in January 2009. I hope things will go well for you.
Inspiron531sと増設したGeForce8400GSの組合せでは、Fedora10のグラフィカルブートスプラッシュ画面を見ることがかなわなかったため、若干の調整を施した。
http://docs.fedoraproject.org/release-notes/f10/ja/
What_is_New_for_Installation_and_Live_Images.htmlを参照しながらの作業になった。
具体的には、カーネルの起動パラメーターにvga=0x318を追加する。つまり、
# vi /boot/grub/grub.conf
でgrub.confを開き、
kernel /vmlinuz-2.6.27.5-117.fc10.x86_64 ro root=UUID=XXXX rhgb quiet vga=0x318
とgrub.confを修正する。但し、UUIDの箇所は、各環境で異なるだろうから、ここではXXXXと表記してあり、実際、初期設定の文字列に一切変更を加える必要がないことを追記する。
カーネルモードセッティングドライバーが使用可能になれば、ネイティブの解像度が得られるとRed Hatが公表している通りだが、テキストベースのプラグインの使用を避けるには、このような経過になることを追記します。
最後になりましたが、この記事が読者の一助になることを祈るばかりです。
では。
Adobeのpdf印刷にも応用が効くことだろうと考えられるが、設定自体は然程入り組んだものではなく、まあ前置きはこれくらいにして本題に入る。
まずgimpをインストールしないことにはポストカードの作成を含めて幅が広がらないことだろう。
$ cd /usr/ports/graphics/gimp
# make install clean
途中エラーが生じたがエラーメッセージを元にビルドに失敗したパッケージを探し、tbzファイルをpkg_addで処理し、インストールが完了した事を追記する。
又、/usr/local/etc/cups/mime.convs の#application/octet-stream application/vnd.cups-raw 0 -の#を外し、application/octet-stream application/vnd.cups-raw 0 -と書き換え保存しないと、印刷の段階でエラーが生じることを追記する。
gimpでcupsのlprを用いるには、何か作成された画像が開かれている下で、ファイル→Print with GutenprintからPrint v5.1.7ウインドウを立ち上げる。
その後、Setup Printer→「Printer Make: Epson」、「Printer Model: Epson PM A820」を選択し、Custom Commandのラジオボタンにチェックを入れた後、コマンド欄に /usr/local/bin/lpr -P PM-T960 と入力してOKボタンを押す。
但しPM-T960の部分はCUPSで設定したプリンター名を入力すれば良く、「/usr/local/bin/lpr -P PM-T960」のコマンドはAdobeのacroreadの印刷の際に利用できることも確認済みであることを追記する。
最後に設定の前提条件を挙げるが、cups及びgutenprintがインストールされ、テスト印刷が可能になっていることを述べる。
上記の記事が年末年始にかけてのポストカード等の印刷の設定の一助となっていることを願うばかりだが、やはりやってみなければ分からないことを含めて諸問題を無事解決される事を祈るばかりである。
では。
色々試した結果なので、最短コースの手解きにならないことを始めにお断りしたい。結論から言えば、表題の件は可能であると述べさせて戴く。
前提条件として、FreeBSD i386 及び cups をインストールしていることを挙げる。cupsのインストールについては、/usr/ports/print/cups にて
# make install clean
で構わないだろう。
そして、PM-T960のドライバをCUPSに組み込むため、gutenprintとgutenprint-cupsをビルドする。
# cd /usr/ports/print/gutenprint-cups
# make install clean
# cd /usr/ports/print/gutenprint
# make install clean
上記がコマンドになる。
但し、foomatic-db-engine-3.0-20070124のビルドで当方の環境ではエラーが出たので、foomatic-db-engineをgoogleで検索し、tbzファイルを入手する必要がある。例えば、http://www.filewatcher.com/m/foomatic-db-engine-3.0.2,1.tbz.37.0.0.html等からダウンロードされたい。インストールのコマンドは、
# pkg_add foomatic-db-engine-20070124,1.tbz
で良いだろう。
AVASYSのホームページから類推できる様に、Linux用のPM-A820のドライバとPM-T960のドライバは互換性がある。そこで、上記、gutenprint, gutenprint-cups のインストールを通じ、CUPSのプリンタ一覧の中に、メーカ:Epson、モデル:
Epson PM A820 - CUPS+Gutenprint v5.1.17 (ja)が追加されていれば良いが、詳細は後で述べる。
Firefoxにて、http://localhost:631/を開き、「プリンタの追加」を選択する。任意の「名前」、「場所」、「説明」を入力した後、「デバイス」で、
「AppSocket/HP JetDirect (Unknown) 」を選択する。「デバイス URI」に
「socket://192.168.1.3:9100」等を入力し、「192.168.1.3」に関しては、PM-T960の「ネットワーク情報確認」にてIPアドレスを確認されたい。「192.168.0.3」等、色々あるだろう。
前段の続きで、「メーカ」に「Epson」を「モデル」に「Epson PM A820 - CUPS+Gutenprint v5.1.17 (ja)」を選択し、「プリンタの追加」ボタンをクリックすれば完了になる。
以上これが決定版と言った書き方をしなかったが、この記事の読者が各自の環境に合わせて、プリンタの設定を済ますことができることを祈るばかりである。
では。
FreeBSD7.1ではJDK15でなくJDK16が要求
される。linux-sun-jdk16ではJAVAのPluginが
Firefox2.0.0.17に認識されないことを追記する。
/usr/ports/distfilesに7つのファイルを置く
ことを要求され、詳細はビルドの際に表示される
エラーメッセージに記される通りで、それぞれ、
jdk-6u3-fcs-bin-b05-jrl-24_sep_2007.jar,
jdk-6u3-fcs-mozilla_headers-b05-unix-24_sep_2007.jar,
jdk-6u3-fcs-src-b05-jrl-24_sep_2007.jar,
tzupdater-1_3_9-2008g.zip, jce_policy-6.zip,
bsd-jdk16-patches-4.tar.bz2,
diablo-caffe-freebsd7-i386-1.6.0_07-b02.tar.bz2
になるが、DL元は全てエラーメッセージに記されて
いるから問題は生じないことを追記する。
ビルドに掛かる時間は2時間前後になり、
休日を利用する形になった。又、portsをupdate
しておかないと、tzupdater-1_3_9-2008g.zipを
読み込ませるために、Makefile, distinfo を修正
する必要があることも追記する。
概ね必要な事を記した気がするが、やはり
やってみなければ分からないことが多いから、
その場その場での修正は必要なことの1つ
だろう。
では。
ドライバはhttp://avasys.jp/index.htmlから
リンクを辿ることにより入手可能。2008/10/2
段階では、pipslite-1.2.0-1.i386.rpmだった。
# rpm -ivh pipslite-1.2.0-1.i386.rpm 後、
GNOMEならば、システム→管理→印刷 で、
プリンター設定画面に移る。
新規プリンター→その他→デバイスURIの入力で、
PM-T960のネットワーク情報確認画面から得られる
IPアドレスを参考にして socket://192.168.1.3:9100
等を入力する。ここで、192.168.1.3は192.168.0.3に
なることもあり、各自の無線環境によって異なる。
その後、プリンターをUSB接続し、コンソール
より、# pipslite-install と入力、PPDファイルを
作成し(詳細はREADME.jaの該当箇所にて)、
CUPSに戻り、PPDファイルを提供ボタンを選択し、
/usr/share/cups/model/ekpmt960.ppd を選択
する。暫く進むと適用ボタンが登場するから、
それをクリックし、設定完了。
但し、この方法はプリンターをUSB接続する
手間が掛かるため、ドライバをインストール後、
http;//localhost:631からCUPSの設定画面に入り、
プリンターの追加、lpd://192.168.1.3/queue、
メーカーでEpson、モデルでEpson LITE, Photo
Image Print System Lite (en)を選択、その後
プリンターの追加ボタンをクリックといった方法
を僕は手っ取り早いせいだろうか採用している。
テスト印刷を済ますまで若干の試行錯誤が
あったもののWindows程インストールに時間を
要しなかったことを記すが、アプリケーション
の幅はやはりWinに分がある様だ。
明日もがんばろう。
では。
SlackwareにSCIM+Anthyをインストールする認識で構わないだろうが、以下記憶を再現しながらのメモ書きになる。
前提条件としてKonquerorで日本語表示が可能であることと日本語ロケールが作成されていることを挙げるが、BackTrack3上の日本語表示について有益なサイトが現時点で複数あるため各自参考にされたいと考える次第。
http://slackpkg.org/からリンクを辿り、slackpkg-2.70.4-noarch-1.tgzをダウンロードする。その後、
# installpkg slackpkg-2.70.4-noarch-1.tgz
でインストール、slackpkgコマンドが使用可になっていることを確認する。以下、断りはないが時宜に応じ再ログインを含む再起動が必要な場合があることを付け加えておく。
slackpkgの設定が必要で/etc/slackpkg/配下にあるmirrorsファイルに
ftp://ftp.riken.jp/Linux/slackware/slackware-current/等、scim関連パッケージを含むサイトを追加する。具体的にはエディタで最後の行にミラーサイトの
アドレスを追加すれば良し。これは時期物のためリンク切れが生じる可能性があることを念頭に置かれたい。
また、slackpkg.confに関しては、エラーが気になるようであれば、CHECKGPG=on をCHECKGPG=off にすれば当面凌げるだろう。
ここからが本題。
# slackpkg update
# slackpkg upgrade gcc
にて関連ファイルをアップグレードしておかないとSCIMを起動する際にエラーメッセージが出る場合がある。
又、gtk+2-2.10.14-i486-1.tgz をhttp://www.filewatcher.com/b/ftp/
192.87.102.42/vol/2/metalab/distributions/ultima/ultimalinux-8.3/x86/l.0.0.html等からダウンロードし、
# slackpkg remove gtk+-1.2.10-i486-4.tgz
# installpkg gtk+2-2.10.14-i486-1.tgz
を行い、Firefox 等のGTK+が関連するパッケージが正常に動作することを確認する必要があったことを追記する。
# slackpkg install scim
上述のコマンドを入力すると、ここで以下の画像は
reinstallのケースのものだが、依存関係を満たすパッケージがインストールされる。
TabキーにてOKとCancelの間を往復されたい。
# slackpkg install anthy
上述のコマンドを入力すると、ここで以下の画像はreinstallのケースのものだが、Anthyがインストールされる。
次にSkimのインストール。http://www.scim-im.org/projects/skimから
リンクを辿り、例えば skim-1.4.5.tar.bz2 等をダウンロードする。
# tar jxvf skim-1.4.5.tar.bz2
# cd skim-1.4.5
# ./configure
# ./scons
# ./scons install
さらに.profileの設定。
export LC_ALL=ja_JP.utf8
export LANG=ja_JP.utf8
export MODIFIERS=@im=SCIM
export QT_IM_MODULE=xim
export GTK_IM_MODULE=scim
scim -d &
skim -d &
を加える。.profileがなければ、例えば root 配下に
新しく作り、上述のコマンドを書き込む。
最後に kasumi について。http://users.zenwalk.org/user-accounts/
tsuren/JP/kasumi-2.2-i486-48.1/等から、kasumi-2.2-i486-48.1.tgz 等を
ダウンロードし、
# installpkg kasumi-2.2-i486-48.1.tgz
再起動すれば、辞書編集機能が有効になっている
だろうが、詳細はSCIM入力メソッドの設定にて。
FirefoxとSCIMの共存については、
# slackpkg upgrade firefox
により2.0→3.0にすることでエラーを回避する
ことができたことを追記する。
以上、書き足りないことがある気がしてならないが長い文章は読む方も大変だろうと考えるのでここまでにする。
記事の読者の皆様がそれぞれの日本語入力環境を無事構築されることを願うばかりだが、やってみなければ分からないことは数多いだろう。
1.1 Requirement: cygwin (gcc, g++, g77, make, gdb )
(#Use cygwin.bat and don't use RXVT,VT102 terminal emulator or you can't go after 1.5.6.)
1.2 Access to http://www.netlib.org/atlas/and obtain atlas3.6.0.gz.
1.3 After downloading atlas3.6.0.gz in /cygwin/usr/local/, unzip atlas3.6.0.gz, when the command line is
$ gunzip -c atlas3.6.0.gz | tar xv
or
$ tar xvfz atlas3.6.0.gz
1.4 Since current directory is /cygwin/usr/local/, move it to /cygwin/usr/local/ATLAS/, when the command line is
$ cd ATLAS
1.5 Build xconfig.exe, when the command line is make and answer the question below appropriately.
1.5.1 160
159
158
...
3
2
1
Enter number at top left of screen [0]: 160
1.5.2 Have you scoped the errata file? [y]: y
1.5.3 Are you ready to continue? [y]: y
1.5.4 Enter your machine type:
1. Other/Unknown
2. AMD Athlon
3. 32 bit AMD Hammer
4. 64 bit AMD Hammer
5. Pentium PRO
6. Pentium Ⅱ
7. Pentium Ⅲ
8. Pentium 4
Enter machine number [1]: 2
1.5.5 enable Posix threads support? [n]: y
1.5.6 Enter the number processors in system [0]: 2
1.5.7 use express setup? [y]: y
1.5.8 Enter Architecture name (ARCH) [WinNT_ATHLONSSE2_2]:
WinNT_ATHLONSSE2_2
1.5.9 Enter Maximum cache size (KB) [4096]: 4096
1.5.10 Enter File creation delay in seconds [0]: 0
1.5.11 Tune the Level 1 BLAS? [y]: y
1.6 Build ATLAS, when the command line is
# make install arch=WinNT_ATHLONSSE2_2
This work will take more than 2.5 hours to complete.
1.7 Copy the library files, when the command lines are given below.
$ cd ./lib/WinNT_ATHLONSSE2_2
# cp *.a /lib
$ ranlib /lib/liblapack.a
$ ranlib /lib/libatlas.a
$ ranlib /lib/libcblas.a
$ ranlib /lib/libf77blas.a
$ ranlib /lib/libptf77blas.a
$ ranlib /lib/libptcblas.a
$ ranlib /lib/libtstatlas.a
1.8 Now you can use ATLAS, when the command lines are given below.
$ g77 -o file01 file01.f -llapack -lf77blas -lcblas -latlas -lg2c -lm
or
$ g95 -o file01 file01.f90 -llapack -lf77blas -lcblas -latlas -lg2c -lm
file01 is an example and you can use other fortran 77 or 95 programs.
2.1 About the LINPACK benchmark
Access to http://www.netlib.org/benchmark/and you can obtain 1000s, 1000d, linpacks, and linpackd, which are benchmark programs. The data which has the largest mflops in the several trials is adopted.
2.1.1 The results from LINPACK 1000s benchmark
$ g77 -o 1000s 1000s.f
| norm resid | resid | machep |
| 9.56832123E+00 | 5.70633099E-04 | 1.19209290E-07 |
| X(1) | X(n) | |
| 1.00003088E+00 | 9.99999046E-01 | |
| factor | solve | total |
| 2.418E+00 | 0.000E+00 | 2.418E+00 |
| mflops | unit | ratio |
| 2.765E+02 | 7.232E-03 | 4.318E+01 |
2.1.2 The results from LINPACK 1000d benchmark
$ g77 -o 1000d 1000d.f
| norm resid | resid | machep |
| 1.05174252E+01 | 1.16766853E-12 | 2.22044605E-16 |
| X(1) | X(n) | |
| 1.00000000E+00 | 1.00000000E+00 | |
| factor | solve | total |
| 2.995E+00 | 0.000E+00 | 2.995E+00 |
| mflops | unit | ratio |
| 2.233E+02 | 8.958E-03 | 5.348E+01 |
2.2 About the DGEMM benchmark
Access to http://www.mcs.anl.gov/index.php, go to Software>MPICH>Win IA32 Binary (1.2.1p1), and obtain mpich2-1.2.1p1-win-ia32.msi. After downloading mpich2-1.2.1p1-win-ia32.msi, we install it on Windows system. Then we add C:\Program Files\MPICH2\bin to path in environment variables, copy libfmpich2g.a, libmpi.a, and libmpicxx.a into /lib, and enter the command lines given below.
$ ranlib /lib/libfmpich2g.a
$ ranlib /lib/libmpi.a
$ ranlib /lib/libmpicxx.a
Then access to https://computecanada.org/ and go to Committees>TECC>Working groups>Benchmarking>Benchmark Collection>Microbenchmarks>DGEMM, and you can obtain dgemm-1.0.0.tar.gz.
$ tar xvfz dgemm-1.0.0.tar.gz
$ cd dgemm-1.0.0
$ cp ./setup/Make.Linux_AtlasFBLAS_Lam ./
We edit Make.Linux_AtlasFBLAS_Lam to solve the problem about Message Passing library (MPI).
$ vi Make.Linux_AtlasFBLAS_Lam
MPlib = -lfmpich2g -lmpi -lmpicxx
# When the value of MPlib was null, it also
# went well.
We build dgemm-1.0.0, when the command line is given below.
$ make arch=Linux_AtlasFBLAS_Lam
Now we can use mpiexec.exe and hpcc-dgemm.exe. Then we will confirm the performance differences ATLAS+BLAS and BLAS which is included in LAPACK using the benchmark software.
$ mpiexec -np 1 hpcc-dgemm 100
Figure1 shows the processing speed of ATLAS+BLAS is approximately 5.6 times faster than the speed of BLAS mentioned above regarding the performance measured by Single DGEMM Gflop/s and the performance differeneces related to the calculation accuracy is not mentioned.
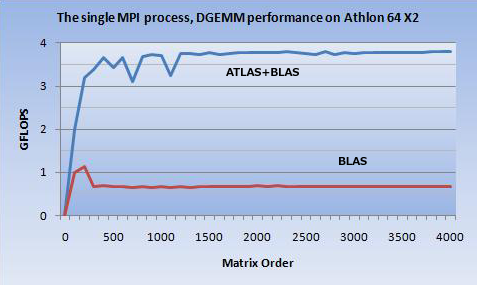
![]() Figure 1 The DGEMM Performance
Figure 1 The DGEMM Performance
Finally, I am happy to assist you in installing ATLAS and the DGEMM benchmark and evaluating the performance differences of some software libraries.
経緯を述べると、先日OSの再インストールの最中に
内蔵CD-ROMドライブが故障したことに気づいた。この
PCはUSB, Removableブートしない10年前の機種だ。
メーカーの技術担当は、既に部品の製造を中止して
おり在庫がなく、修復不能な旨告げるのみだった。されど、
FDドライブとHDドライブは辛うじてブートする。
内蔵CD-ROMドライブの読み取りに故障を抱えている
のみだから、手持ちのWindowsXPのCD(製品版)とFD
ブート、外付けのCD-ROMドライブがあればうまくいく例が
あることを以下に記す。
利用したCD-ROMドライブは、I-O DATAのDVDP-U8P、
ポータブルDVDドライブでブート対応している。PCは富士通の
FMV-DESKPOWER C2/507、1999年モデルでUSBブート等
の機能はない。
マイクロソフトのWindows XPのインストール用起動ディスク
を作成しhttp://support.microsoft.com/kb/880422/ja
(計6枚)準備完了、DVDP-U8Pはsysファイル等のドライバ
を用意していないが、MSの起動ディスクの中身が完全に
代用してくれる形となった。
ポータブルDVDドライブのACパワーをオンにし、PC固有の
USBにケーブルを接続、PCの電源をオンにし、FDブートを選択、
インストール用起動ディスクを順番に入れ、6枚目で画面に変化
が生じ、以下、その指示に従いXPのインストールを選択すると、
通常のMS-DOS起動ディスクでは認識しない外付けのCD-ROM
ドライブ(ポータブルDVDドライブ)を認識し、1時間程でイン
ストール完了といった成功例に繋がるだろうか。
上記の内容は富士通のHPにも掲載例があるが、
http://www.fmworld.net/biz/fmv/winxp/matter/r160.html
若干手順が異なるので、ここに記した。DVDP-U8Pもメーカー
HPは動作不能としているがOSがWindows98のケースであり、
XPでは不具合を現段階では確認していないことを記す。
ささやかな記事ではありますが、皆様のお役に立てることを
願っております。
Specifications for this machine tell us its memory is 512MB or 1GB. This machine I selected indeed has two 512MB memories. Picture A shows two preinstalled 512MB memories work normally. The software package for this verification is Memtest86 (http://www.memtest86.com, Download-Memtest86 v3.4a ISO image(zip)).
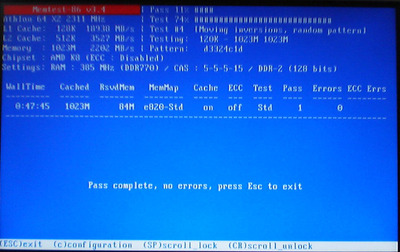
![]() Picture A
Picture A
At the same time, there are well-known things in the things specifications for this machine don't tell us. Its memory capacity is above 1GB and can be 2GB. Picture B shows two 2GB memories work
normally.
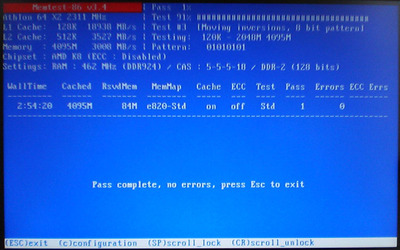
![]() Picture B
Picture B
Memories used in this verification are DDR2 PC2-6400 2GB x2 (Pulsar DCDDR2-4GB-800).
The sample concordance lines are on the popup window.
When the security tab on the Norton Internet Security
is off, I can display the concordance lines and use the
Collocation Sampler. Although I don't want you to run
a risk, I cannot now offer the better solutions than what
I mentioned here to display the sample concordance
lines from the Collins Corpus. Good luck!
Here we can visually understand the convergence of Cauchy sequence by entering the value of x and N. Definition: The function f(x,N,i) of two positive integers x, i and a rational number N is defined by
![f\left(x,N,i\right)=\frac{\left[N\exp\left(0.01i-10\right){}r\left(x\right)\right]}{N\exp\left(0.01i-10\right)}](http://paulownia.sakura.ne.jp/materials/learning_journals/archives/f_cs.png) .
.
The function g(N,i) of a positive integer i and a rational number N is defined by
![]() .
.
[•] is Gauss' symbol and r(x) is a positive square root of x. The vertical axis shows a sequence of values on the function of (x,N,i). The horizontal axis shows a sequence of values on the function of (N,i). The function of (x,N,i) has a minimum value in the assigned (i=1) condition and a maximum value in the assigned (i=1000) condition when the domain of i is between 1 and 1000.
The domain of x is over 0 and below 10^8, and the domain of N is over 0.1^16 and below 10^16. When you enter the numerical values of x and N, please push the enter key each time you enter x or N in the text box.
If you enter the value of x and N in other domains, the program automatically sets the variables such as x=10^5 and N=10^5.
source code: CauchySequence.java
import java.math.BigDecimal;
import java.math.BigInteger;
import java.awt.*;
import java.awt.event.*;
import java.applet.Applet;
import javax.swing.JLabel;
import javax.swing.JTextField;
public class CauchySequence extends Applet implements ActionListener{
private static final long serialVersionUID = -6724959421340457497L;
JTextField yx = new JTextField("100000");
JTextField yn = new JTextField("100000");
JLabel label1 = new JLabel("Convergence of Cauchy sequence", JLabel.CENTER);
JLabel label2 = new JLabel("A natural number, 0<x<10^8", JLabel.CENTER);
JLabel label3 = new JLabel("A rational number, 0.1^16<N<10^16", JLabel.CENTER);
// variable set
double x = 100000;
double n = 100000;
public void init(){
label1.setPreferredSize(new Dimension(416,24));
label1.setFont(new Font("Serif",Font.BOLD,14));
add(label1);
label2.setPreferredSize(new Dimension(170,23));
label2.setFont(new Font("Serif",Font.BOLD,11));
add(label2);
yx.setPreferredSize(new Dimension(80,23));
add(yx);
label3.setPreferredSize(new Dimension(210,23));
label3.setFont(new Font("Serif",Font.BOLD,11));
add(label3);
yn.setPreferredSize(new Dimension(120,23));
add(yn);
yx.addActionListener(this);
yn.addActionListener(this);
}
public void actionPerformed(ActionEvent e){
if(e.getSource()==yx){
x=Double.valueOf(yx.getText()).doubleValue();
if(x <= 0 || x >= Math.pow(10.0,8) || x!=(long)x){
x=100000;
}
}
if(e.getSource()==yn){
n = Double.valueOf(yn.getText()).doubleValue();
BigDecimal n0 = new BigDecimal(yn.getText());
BigDecimal n1 = new BigDecimal(Math.pow(0.1,16));
BigDecimal n2 = new BigDecimal(Math.pow(10.0,16));
int d1 = n0.compareTo(n1);
int d2 = n0.compareTo(n2);
if(d1==-1 || d1==0 || d2==0 || d2==1){
n=100000;
}
}
yx.setText(""+(long)x);
yn.setText(""+n);
repaint();
}
public void paint(Graphics g){
// variable set
int i;
double b, m, p, y, minp, maxp, minb, maxb;
BigDecimal a0, a2, b0, n0, p0, p1, x0;
BigInteger a1;
double[] pp = new double[1000];
double[] bb = new double[1000];
int[] xxx = new int[1000];
int[] yyy = new int[1000];
for(i=1;i<=1000;i++){
p = Math.exp(10-0.01*i);
m = n/p;
p0 = new BigDecimal(p);
n0 = new BigDecimal(n);
p1 = n0.divide(p0,30,BigDecimal.ROUND_HALF_EVEN);
pp[i-1] = Math.log(m);
y = Math.sqrt(x);
x0 = new BigDecimal(y);
a0 = x0.multiply(p1);
a1 = a0.toBigInteger();
a2 = new BigDecimal(a1);
b0 = a2.divide(p1,30,BigDecimal.ROUND_HALF_EVEN);
b = b0.doubleValue();
bb[i-1] = b;
}
minp = pp[0];
maxp = pp[0];
minb = bb[0];
maxb = bb[0];
for(i=0;i<=999;i++){
if(pp[i]>maxp){
maxp = pp[i];
}
}
for(i=0;i<=999;i++){
if(pp[i]<minp){
minp = pp[i];
}
}
for(i=0;i<=999;i++){
if(bb[i]>maxb){
maxb = bb[i];
}
}
for(i=0;i<=999;i++){
if(bb[i]<minb){
minb = bb[i];
}
}
for (i=0;i<=999;i++){
double xx = maxp-minp;
double yy = maxb-minb;
xxx[i] = (int)((pp[i]-minp)*(351/xx))+33;
yyy[i] = 441-(int)((bb[i]-minb)*(351/yy));
}
Graphics2D g2 = (Graphics2D)g;
GradientPaint gp1 = new GradientPaint(0, 0, new Color(154,181,228), 0,470,new Color(225,232,245), true);
g2.setPaint(gp1);
g2.fillRect(0,0,416,470);
super.paint(g);
GradientPaint gp2 = new GradientPaint(0, 33, new Color(225,232,245), 0,351,new Color(154,181,228), true);
g2.setPaint(gp2);
g2.fillRect(33,90,354,351);
g2.setColor (Color.black);
g2.setFont(new Font ("Serif",Font.PLAIN,11));
g2.drawString("f",15,95);
g2.drawString("(x,N,i)",1,108);
g2.drawString("g(N,i)",365,455);
for (i=0;i<=998;i++){
g.drawLine(xxx[i], yyy[i], xxx[i+1], yyy[i+1]);
}
}
}
I have recently begun to code the examples of numerical computation in Java and hope to make better use of the computational power and the graphical user interface.
1. Requirement: cygwin ( gcc, g++, g77, make, gdb )
2. Access to http://www.netlib.org/lapack/ and obtain lapack-3.1.1.gz.
3. After downloading lapack-3.1.1.gz in /cygwin/home/***/, unzip lapack-3.1.1.gz, when the command line is
$ gunzip -c lapack-3.1.1.gz | tar xv
or
$ tar xvfz lapack-3.1.1.gz
Since current directory is /cygwin/home/***/, move it to /cygwin/home/***/lapack-3.1.1/, when the command line is
$ cd lapack-3.1.1
5. Copy and modify make.inc.LINUX, when the command line is given below.
$ cp INSTALL/make.inc.LINUX ./make.inc
6. Modify make.inc, using your text editor.
<EXAMPLE>
NOOPT = -ffloat-store
# The above line is necessary when using g95.
BLASLIB = $(HOME)/lapack-3.1.1/blas$(PLAT).a
LAPACKLIB = lapack$(PLAT).a
TMGLIB = tmglib$(PLAT).a
EIGSRCLIB = eigsrc$(PLAT).a
LINSRCLIB = linsrc$(PLAT).a
7. Build BLAS library and LAPACK library, when the command lines are
$ make blaslib
and
$ make lapacklib
If neither blas_LINUX.a nor lapack_LINUX.a were made in your current directory, modify make.inc appropriately.
8. Copy and modify blas_LINUX.a and lapack_LINUX.a, when the command lines are
$ cp blas_LINUX.a /lib/libblas.a
$ cp lapack_LINUX.a /lib/liblapack.a
$ ranlib /lib/libblas.a
$ ranlib /lib/liblapack.a
9. Now you can use LAPACK, when the command line is
$ g77 -o file01 file01.f -llapack -lblas -lg2c -lm
where file01.f were an example and you can use other fortran77 programs.
 2005年6月28日に英語版が発表
2005年6月28日に英語版が発表
され、2006年9月12日に日本語版
が発表されたフリー・ソフト(一部
機能を追加すると有料になる)に
はっとさせられる1日だった。
右図は、我が家周辺の地図を
取り込んだものだが、プライバ
シーを考慮し、緯度・経度情報は
割愛させていただいたが、ゼンリンの地道な努力があってからか、
このポリゴンのリアリティは我が家そのもの。
フライト・シミュレーターが好きな方々には理解して
いただけると思うが、ルート機能が日本語版で有効に機能する
ならば、確実に、現在のカー・ナビの水準は越えるだろう(いや、
これは言い過ぎで、実際は音声の誘導など全く付随していない
のだが)と想像力を逞しく発展させる時間に浸りがち...
これではイカン。
やっぱり、一目で分かる技術の進歩が世界に貢献する姿と
いうものは斯くあるべしだなと、久しぶりに興奮の余韻の
冷め遣らない、いや現実に戻らなければとの思いも交錯する
中、今日一日、この狭い世界の中だけ...と、開発者
でもないのに喜んでいる私は何者だろうか?
ここからが今日の課題。
TOEIC対策は模試。正答率は、パート1が8/10、
パート2が6/10で、パート5が17/20。パート1
・2のナレーションの間、先読みできた設問の数、36個
と少な目。パート5の20題を解くのに要した時間は10分
5秒。まだ、ペースは上がっていない。ここからだ。
仏検対策は文法とディクテ。正答率は、文法が16/30で、
ディクテが19/32。接続詞の用法に熟達すること、細部に
わたり聞き逃さない耳を鍛えることが今日の課題。
明日もがんばろう。
では。
